This report gives the Fractional Increase in CI (Confidence Interval) Length and Relative Std (Standard) Error of Estimate for each parameter estimate in the model. Estimation Efficiency Outline shows the Estimation Efficiency outline for the Bounce Data.jmp sample data table, located in the Design Experiment folder.
The covariance matrix for the ordinary least squares estimator is σ2(X’X)-1. The diagonal elements of (X’X)-1 are the relative variances (the variances divided by σ2) of the parameter estimates. For two-level designs and using the effects coding convention (see Coding in Column Properties), the minimum value of the relative variance for any parameter estimate is 1/n, where n is the number of runs. This occurs when all the effects for the design are orthogonal and the design is D-optimal.
Let 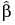 denote the vector of parameter estimates. The ideal design, which may not exist, is a design whose covariance matrix is given as follows:
denote the vector of parameter estimates. The ideal design, which may not exist, is a design whose covariance matrix is given as follows:
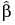 denote the vector of parameter estimates. The ideal design, which may not exist, is a design whose covariance matrix is given as follows:
denote the vector of parameter estimates. The ideal design, which may not exist, is a design whose covariance matrix is given as follows:Specifically, for the ith parameter estimate, the Fractional Increase in Confidence Interval Length is defined as follows:
σ2 is the unknown response variance,
n is the number of runs.
The Relative Std Error of Estimate gives the ratio of the standard deviation of a parameter’s estimate to the error standard deviation. These values indicate how large the standard errors of the model’s parameter estimates are, relative to the error standard deviation. For the ith parameter estimate, the Relative Std Error of Estimate is defined as follows:


 is the
is the 

 is the
is the  , and
, and
 is the
is the  .
.