Note: For -LogLikelihood, BIC, AICc, and ERIC, smaller is better. For more details, see Likelihood, AICc, and BIC in Statistical Details.
(Available only for exponential family distributions and when the Lasso or adaptive Lasso estimation method is specified.) The Extended Regularization Information Criterion: 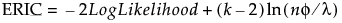 where λ is the value of the tuning parameter and φ is the nuisance parameter. See Hui et al. (2015).
where λ is the value of the tuning parameter and φ is the nuisance parameter. See Hui et al. (2015).
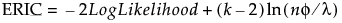 where λ is the value of the tuning parameter and φ is the nuisance parameter. See Hui et al. (2015).
where λ is the value of the tuning parameter and φ is the nuisance parameter. See Hui et al. (2015).(Not available for Quantile Regression.) An extension of the RSquare measure that can be applied to general regression models. Generalized RSquare compares the likelihood of the fitted model (LM) to the likelihood of the intercept-only (constant) model (L0). It is scaled to have a maximum of 1. For distributions other than Binomial, the Generalized RSquare is defined as follows:
A Generalized RSquare value of 1 indicates a perfect model; a value of 0 indicates a model that is no better than a constant model. The Generalized RSquare measure simplifies to the traditional RSquare for continuous normal responses in the standard least squares setting. Generalized RSquare is also known as the Nagelkerke or Craig and Uhler R2, which is a normalized version of Cox and Snell’s pseudo R2. See Nagelkerke (1991).



 .
. .
.
