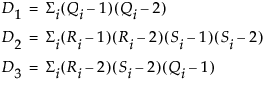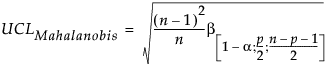Multivariate Methods • Correlations and Multivariate Techniques • Computations and Statistical Details
Previous
 • 
Next
Computations and Statistical Details
Estimation Methods
Robust
This method essentially ignores any outlying values by substantially down-weighting them. A sequence of iteratively reweighted fits of the data is done using the weight:
wi = 1.0 if Q < K and wi = K/Q otherwise,
where K is a constant equal to the 0.75 quantile of a chi-square distribution with the degrees of freedom equal to the number of columns in the data table, and
where yi = the response for the ith observation, μ = the current estimate of the mean vector, S2 = current estimate of the covariance matrix, and T = the transpose matrix operation. The final step is a bias reduction of the variance matrix.
The tradeoff of this method is that you can have higher variance estimates when the data do not have many outliers, but can have a much more precise estimate of the variances when the data do have outliers.
Pearson Product-Moment Correlation
The Pearson product-moment correlation coefficient measures the strength of the linear relationship between two variables. For response variables X and Y, it is denoted as r and computed as
If there is an exact linear relationship between two variables, the correlation is 1 or –1, depending on whether the variables are positively or negatively related. If there is no linear relationship, the correlation tends toward zero.
Nonparametric Measures of Association
For the Spearman, Kendall, or Hoeffding correlations, the data are first ranked. Computations are then performed on the ranks of the data values. Average ranks are used in case of ties.
Spearman’s ρ (rho) Coefficients
Spearman’s ρ correlation coefficient is computed on the ranks of the data using the formula for the Pearson’s correlation previously described.
Kendall’s τb Coefficients
Kendall’s τb coefficients are based on the number of concordant and discordant pairs. A pair of rows for two variables is concordant if they agree in which variable is greater. Otherwise they are discordant, or tied.
The formula
computes Kendall’s τb where:
Note the following:
•
The sgn(z) is equal to 1 if z>0, 0 if z=0, and –1 if z<0.
•
The ti (the ui) are the number of tied x (respectively y) values in the ith group of tied x (respectively y) values.
•
The n is the number of observations.
•
Kendall’s τb ranges from –1 to 1. If a weight variable is specified, it is ignored.
Computations proceed in the following way:
•
Observations are ranked in order according to the value of the first variable.
•
The observations are then re-ranked according to the values of the second variable.
•
The number of interchanges of the first variable is used to compute Kendall’s τb.
Hoeffding’s D Statistic
The formula for Hoeffding’s D (1948) is
where:
Note the following:
•
The Ri and Si are ranks of the x and y values.
•
The Qi (sometimes called bivariate ranks) are one plus the number of points that have both x and y values less than the ith points.
•
A point that is tied on its x value or y value, but not on both, contributes 1/2 to Qi if the other value is less than the corresponding value for the ith point. A point tied on both x and y contributes 1/4 to Qi.
When there are no ties among observations, the D statistic has values between –0.5 and 1, with 1 indicating complete dependence. If a weight variable is specified, it is ignored.
Inverse Correlation Matrix
The inverse correlation matrix provides useful multivariate information. The diagonal elements of the inverse correlation matrix, sometimes called the variance inflation factors (VIF), are a function of how closely the variable is a linear function of the other variables. Specifically, if the correlation matrix is denoted R and the inverse correlation matrix is denoted R-1, the diagonal element is denoted rii and is computed as
where Ri2 is the coefficient of variation from the model regressing the ith explanatory variable on the other explanatory variables. Thus, a large rii indicates that the ith variable is highly correlated with any number of the other variables.
Distance Measures
The Outlier Analysis plots show the specified distance measure for each point in the data table.
Mahalanobis Distance Measures
The Mahalanobis distance takes into account the correlation structure of the data and the individual scales. For each value, the Mahalanobis distance is denoted Mi and is computed as
where:
Yi is the data for the ith row
Y is the row of means
S is the estimated covariance matrix for the data
The UCL reference line (Mason and Young, 2002) drawn on the Mahalanobis Distances plot is computed as
where:
n = number of observations
p = number of variables (columns)
= (1–αth) quantile of a Beta distribution
If a variable is an exact linear combination of other variables, then the correlation matrix is singular and the row and the column for that variable are zeroed out. The generalized inverse that results is still valid for forming the distances.
Jackknife Distance Measures
The jackknife distance is calculated with estimates of the mean, standard deviation, and correlation matrix that do not include the observation itself. For each value, the jackknife distance is computed as
where:
n = number of observations
p = number of variables (columns)
Mi = Mahalanobis distance for the ith observation
The UCL reference line (Penny, 1996) drawn on the Jackknife Distances plot is calculated as
T2 Distance Measures
The T2 distance is the square of the Mahalanobis distance, so Ti2 = Mi2.
The UCL on the T2 distance is:
where
n = number of observations
p = number of variables (columns)
= (1–αth) quantile of a Beta distribution
Multivariate distances are useful for spotting outliers in many dimensions. However, if the variables are highly correlated in a multivariate sense, then a point can be seen as an outlier in multivariate space without looking unusual along any subset of dimensions. In other words, when the values are correlated, it is possible for a point to be unremarkable when seen along one or two axes but still be an outlier by violating the correlation.
Cronbach’s α
Cronbach’s α is defined as
where
k = the number of items in the scale
c = the average covariance between items
v = the average variance between items
If the items are standardized to have a constant variance, the formula becomes
where
r = the average correlation between items
The larger the overall α coefficient, the more confident you can feel that your items contribute to a reliable scale or test. The coefficient can approach 1.0 if you have many highly correlated items.