Launch the Life Distribution Platform

Launch the Life Distribution platform by selecting Analyze > Reliability and Survival > Life Distribution.

•	The Life Distribution tab models ungrouped data. The following types of reports can result:

‒	The Life Distribution report appears when you do not specify a Failure Cause role. From this report, you can compare common distributions and examine statistics. See Life Distribution Report.

‒	The Weibayes report appears when you have zero failures in your data. See Weibayes Report.

‒	The Competing Cause report appears when you specify a Failure Cause role. In addition to the features in the Life Distribution report, you can also compare individual failure causes. See Competing Cause Report.

Note: You can examine Fixed Parameter and Bayesian models in the Life Distribution and Competing Cause reports.

•

The Compare Groups tab enables you to specify a Grouping variable. The Compare Groups report compares different groups using a single specified distribution. For example, you might compare Weibull fits for components grouped by supplier. In contrast, the Life Distribution tab compares several fitted distributions for a single group. See Life Distribution - Compare Groups Report.

Launch Window Options

The launch window contains the following options:

Y, Time to Event

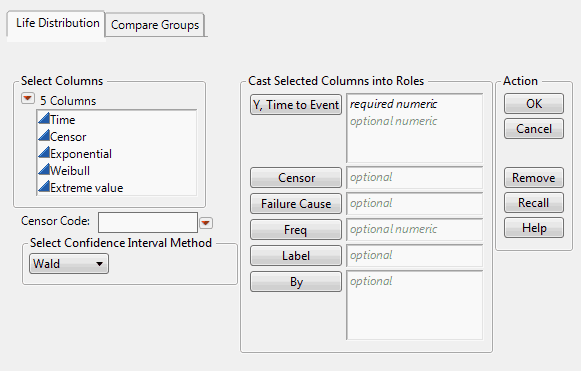
The time to event (such as the time to failure) or time to right censoring. For interval censoring, specify two Y variables, where one Y variable gives the lower limit and the other Y variable gives the upper limit for each unit. For details about censoring, see Event Plot.

Grouping

(Appears only in the Compare Groups tab.) A column containing the groups that you want to compare. For an example, see Examine the Same Distribution across Groups.

Censor

A column that identifies right-censored observations. Select the value that identifies right-censored observations from the Censor Code menu beneath the Select Columns list. The Censor column is used only when one Y is entered.

Failure Cause

A column that contains multiple failure causes. If a Failure Cause column is selected, then a section is added to the window:

‒	Check boxes appear that allow the failure mode to use ZI distributions, TH distributions, DS distributions, fixed parameter models or Bayesian models for the analysis.

‒

Distribution specifies the initial distribution to fit for each failure cause. Select one distribution to fit for all causes; select Individual Best to let the platform automatically choose the best fit for each cause; or select Manual Pick to manually choose the distribution to fit for each failure cause after JMP creates the Life Distribution report. You can also change the distribution fits in the Life Distribution report itself.

‒

Comparison Criterion is an option that appears only when you choose the Individual Best distribution fit. Select the method by which JMP chooses the best distribution: Corrected Akaike Information Criterion (AICc), Bayesian Information Criterion (BIC), or -2Loglikelihood. For more details, see Fitting Linear Models. You can change the method later in the Model Comparisons report. See Model Comparisons for details.

‒	Censor Indicator in Failure Cause Column identifies the indicator used in the Failure Cause column for observations that did not fail. To specify such an indicator, select this option and then enter the indicator in the box that appears.

See Meeker and Escobar (1998, chap. 15) for a discussion of multiple failure causes. Omit Competing Causes illustrates how to analyze multiple causes.

Freq

A column that contains frequencies or observation counts when the information in a row represents multiple units. If the value in a row is 0 or a positive number, then the value represents the frequencies or counts of observations for that row.

Label

A column that contains identifiers other than the row number. These labels appear on the y axis in the event plot.

An optional variable whose levels define rows used to create separate models.

Censor Code

After selecting the Censor column, select the value that designates right-censored observations from the list. Missing values are excluded from the analysis. JMP attempts to detect the censor code and display it in the list.

Select Confidence Interval Method

Defines the method used for computing confidence intervals for the parameters. The default is Wald, but you can select Likelihood instead. However, all confidence intervals provided in the profilers are based on the Wald method. This is done to reduce computation time. For more information, refer to Estimation and Confidence Intervals.

Failure Distribution by Cause

Appears only in the Life Distribution tab when a Cause is specified. Specify which families of distributions should be available to model the life distributions for individual causes. Select an initial distribution, Individual Best, or Manual Pick from the Distribution menu. For details, see Failure Cause.