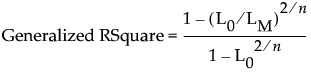Fitting Linear Models • Generalized Regression Models • Model Fit Reports
Previous
 • 
Next
Model Fit Reports
For each Estimation Method and Validation Method that you specify in the Model Launch panel, a report is produced. The report specifies your selected Estimation and Validation methods in its title.
The following reports are presented by default:
•
Model Summary
•
Estimation Details (shown only for Lasso, Elastic Net, and Ridge)
•
Solution Path (shown for all but the Maximum Likelihood Estimation Method and Quantile Regression)
•
Parameter Estimates for Centered and Scaled Predictors
•
Parameter Estimates for Original Predictors
•
Effect Tests
Model Summary
The Model Summary report describes the model that you have fit and provides summary information about the fit itself.
Model Description Detail
The first part of the Model Summary report gives information that describes the model that you have fit.
Response
The column assigned to the Y role in the Fit Model window.
Distribution
The Distribution selected in the Fit Model window. For Quantile Regression, the value of the specified quantile for the response is also displayed.
Estimation Method
The Estimation Method selected in the Model Launch panel.
Validation Method
The Validation Method selected in the Model Launch panel.
Mean Model Link
The link function for the model for the mean, based on the Distribution selected in the Fit Model window.
Location Model Link
The link function for the model for the location parameter, shown when Cauchy is selected as the Distribution in the Fit Model window.
Scale Model Link
The link function for the model for the scale parameter, based on the Distribution selected in the Fit Model window.
Probability Model Link
The link function for the model for the probability, based on the Distribution selected in the Fit Model window.
Dispersion Model Link
The link function for the model for the dispersion parameter, based on the Distribution selected in the Fit Model window.
Zero Inflation Model Link
The link function for the model for the zero inflation parameter, based on the Distribution selected in the Fit Model window.
Model Fit Detail
The second part of the Model Summary report gives statistics related to the model fit. If either Holdback or Validation Column is selected as the Validation Method, these statistics are computed separately for the training and validation sets. This part of the Model Summary report is not available if either KFold or Leave-One-Out is selected as the Validation Method.
Number of rows
The number of rows.
Sum of Frequencies
The sum of the values of a column assigned to the Freq or Weight role in the Fit Model window.
Note: For -LogLikelihood, BIC, and AICc, smaller is better. For more details, see Likelihood, AICc, and BIC in Statistical Details.
-LogLikelihood
The negative of the natural logarithm of the likelihood function for the specified model.
Note: -LogLikelihood is not available for Quantile Regression.
Objective Function
The value of the function that is minimized to fit the specified quantile regression model. Only displayed for Quantile Regression.
BIC
The Bayesian Information Criterion: .
AICc
The corrected Akaike Information Criterion: .
Generalized RSquare
An extension of the RSquare measure that can be applied to general regression models. Generalized RSquare compares the likelihood of the fitted model (LM) to the likelihood of the intercept-only (constant) model (L0). It is scaled to have a maximum of 1. The Generalized RSquare is defined as follows:
A Generalized RSquare value of 1 indicates a perfect model; a value of 0 indicates a model that is no better than a constant model. The Generalized RSquare measure simplifies to the traditional RSquare for continuous normal responses in the standard least squares setting. Generalized RSquare is also known as the Nagelkerke or Craig and Uhler R2, which is a normalized version of Cox and Snell’s pseudo R2. See Nagelkerke (1991).
Note: Generalized RSquare is not available for Quantile Regression.
Caution: You should not compare Generalized RSquare values for models that use different response distributions. The comparison being made is to the intercept-only model with a given response distribution.
Estimation Details
The Estimation Details report shows the settings of the Advanced Controls for the Lasso, Elastic Net, and Ridge estimation methods. For more information about these controls, see Advanced Controls.
Solution Path
The Solution Path report plots the estimated parameter values against the magnitude of the scaled parameter estimates. Estimates with large values for the Magnitude of Scaled Parameter Estimates are close to the MLE. Estimates with small values are heavily penalized. The value of the tuning parameter increases as the Magnitude of Scaled Parameter Estimates decreases.
You can select paths in the Solution Path plot to highlight the corresponding terms in the Parameter Estimates for Centered and Scaled Predictors and in the Parameter Estimates for Original Data reports. This action also selects the corresponding columns in the data table. Selecting rows in either of the reports highlights the corresponding rows in the other report and the corresponding paths in the Solution Path plot. Press Shift and click to select multiple paths or rows.
Next to the Solution Path plot is the Validation Plot, a plot of the goodness of fit of the model. This graph plots the magnitude of the scaled parameter estimates against values corresponding to the selected validation method. This report appears for all Estimation Methods except Maximum Likelihood and all Distributions except Quantile Regression.
The Parameter Estimates are plotted using the vertical axis of the Solution Path plot. These are the scaled parameter estimates. They are derived for a model expressed in terms of centered and scaled predictors (see Parameter Estimates for Centered and Scaled Predictors).
The horizontal scaling for the Solution Path and Validation plot is given in terms of the Magnitude of Scaled Parameter Estimates. This is the l1 norm, defined as the sum of the absolute values of the scaled parameter estimates for the model for the mean. (Estimates corresponding to the intercept, dispersion parameters, and zero-inflation parameters are excluded from the calculation of the l1 norm.) A vertical red line is placed at the value of the l1 norm for the solution displayed in the Parameter Estimates for Original Predictors report.
The Solution Path plot and Validation Plot are interactive. You can drag the arrow at the top of the vertical red line in either plot to change the magnitude of the penalty (and the corresponding model). In the Validation Plot, you can also drag the arrow or click anywhere in the plot to change the model. As you drag the vertical red line to change the model, the results in the report update to reflect the currently selected model.
When the number of predictors is less than the number of observations, the Solution Path plot usually shows the entire range of estimates from zero to the unpenalized fit given by the MLE. Otherwise, the plot extends to a magnitude that is close to the unpenalized solution. This occurs when the jump from the next-to-last grid point to the MLE solution is so large that the detail for solutions up to the next-to-last point is obscured. When this happens, as long as the MLE is not the final solution, the Solution Path plot is rescaled so that the axis extends only to the next-to-last grid point.
The Validation Plot vertical axis varies based on the Validation Method chosen. Validation Plot Vertical Axis by Validation Method illustrates the vertical axis by Validation Method. For all vertical axis options, lower values are better. A vertical red line is placed at the value of the l1 norm tuning parameter for the solution displayed in the Parameter Estimates for Original Predictors report. There is some room for adjustment of the tuning parameter. You can move the red vertical line to the left or right to adjust the tuning parameter. A dashed vertical line remains at the best fit model. For AICc, BIC, KFold, and Leave-One-Out validation methods, the graph indicates regions where the tuning parameter is best kept.
For AICc and BIC validation methods, two regions are shown in the plot.
•
The green region indicates there is strong evidence that the model is as good as the best model.
•
The yellow region indicates there is weaker evidence that the model is sufficient.
Using a model where the tuning parameter falls outside these bounds is not recommended. See Burnham and Anderson (2002).
The KFold and Leave-One-Out validation methods show one green region based on standard error. Any model within one standard error of the best model is considered similar to the best. It is not recommended to use a model with the tuning parameter out of these bounds.
Tip: You can use the green region to help select a simpler model that is no worse than the best model.
Validation Plot Vertical Axis by Validation Method 
Validation Method
Vertical Axis
Tuning Parameter Regions
KFold
Scaled -LogLikelihood
One
Holdback
Scaled -LogLikelihood
None
Leave-One-Out
Scaled -LogLikelihood
One
BIC
BIC
Two
AICc
AICc
Two
Validation Column
Scaled -LogLikelihood
None
Parameter Estimates for Centered and Scaled Predictors
Tip: You can click on terms in the Parameter Estimates for Centered and Scaled Predictors report to highlight the corresponding paths in the Solution Path plot. The corresponding columns in the data table are also selected. This is useful in terms of running further analyses. Press Shift and click the terms to select multiple rows.
For all fits in the Generalized Regression personality, every predictor is centered to have mean zero and scaled to have sum of squares equal to one:
•
The mean is subtracted from each observation.
•
Each difference is then divided by the square root of the sum of the squared differences from the mean.
This puts all predictors on an equal footing relative to the penalties applied.
Note: When the No Intercept option is selected in the launch window, the predictors are not centered and scaled.
The Parameter Estimates for Centered and Scaled Predictors report gives parameter estimates for the model expressed in terms of the centered and scaled predictors. The estimates are determined by the Validation Method that you specified. The estimates are depicted in the Solution Path plots by a vertical red line.
The report provides the following information:
Term
A list of the model terms.
Estimate
The parameter estimate corresponding to the centered and scaled model term.
Std Error
The standard error of the estimate. This is obtained using M-estimation and a sandwich formula (Zou, 2006, and Huber and Ronchetti, 2009).
Wald ChiSquare
The ChiSquare value for a Wald test of whether the parameter is zero.
Prob > ChiSquare
The p-value for the Wald test.
Lower 95%
The lower bound for a 95% confidence interval for the parameter. Note that you can change the alpha level in the Fit Model window by selecting Set Alpha Level from the red triangle menu.
Upper 95%
The upper bound for a 95% confidence interval for the parameter. Note that you can change the alpha level in the Fit Model window by selecting Set Alpha Level from the red triangle menu.
Parameter Estimates for Original Predictors
Tip: You can select terms in the Parameter Estimates for Original Predictors report to highlight the corresponding paths in the Solution Path plot. The corresponding columns in the data table are also selected. This is useful when running further analyses. Press Shift and click the terms to select multiple rows.
The Parameter Estimates for Original Predictors report gives parameter estimates for the model expressed in terms of the original (uncentered and unscaled) predictors.
The report provides the following information:
Term
A list of the model terms. “Forced in” appears next to any terms that were forced into the model using the Advanced Controls option.
Estimate
The parameter estimate corresponding to the model term given in terms of the original measurements.
Std Error
The standard error of the estimate. This is obtained using M-estimation and a sandwich formula (Zou, 2006, and Huber and Ronchetti, 2009).
Wald ChiSquare
The ChiSquare value for a Wald test of whether the parameter is zero.
Prob > ChiSquare
The p-value for the Wald test.
Lower 95%
The lower bound for a 95% confidence interval for the parameter. Note that you can change the alpha level in the Fit Model window by selecting Set Alpha Level from the red triangle menu.
Upper 95%
The upper bound for a 95% confidence interval for the parameter. Note that you can change the alpha level in the Fit Model window by selecting Set Alpha Level from the red triangle menu.
Effect Tests
The Effect Tests report gives the following information:
Source
A list of the effects in the model.
Nparm
The number of parameters associated with the effect.
DF
The degrees of freedom for the Wald ChiSquare test. This is the number of nonzero parameter estimates associated with the effect in the model.
Wald ChiSquare
The ChiSquare value for a Wald test of whether all parameters associated with the effect are zero.
Prob > ChiSquare
The p-value for the Wald ChiSquare test.
If the coefficient for an effect has been estimated as zero, then:
•
If the effect has one degree of freedom, the word “Removed” appears at the far right in the row for that effect.
•
If the effect has multiple degrees of freedom, the phrase “Levels removed” appears, followed by the number of levels that correspond to terms with parameter estimates of zero.