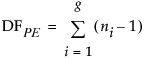|
Shows a report containing the parameter estimates and t tests for the hypothesis that each parameter is zero. See Parameter Estimates.
|
|
JMP Learning Library – Basic Inference - Proportions and Means
Watch a brief video on how to perform a one-way analysis of variance and interpret the F-statistic.
Watch a brief video on how to perform a one-way analysis of variance and interpret the F-statistic.
The Summary of Fit report provides details such as RSquare calculations and the AICc and BIC values.
|
Estimates the proportion of variation in the response that can be attributed to the model rather than to random error. Using quantities from the corresponding Analysis of Variance table, RSquare (also called the coefficient of multiple determination) is calculated as:
|
|
Note: If either a Frequency or a Weight variable is entered in the Fit Model launch window, the entries in the Analysis of Variance report are adjusted in keeping with the descriptions in Frequency and Weight.
|
Gives the associated degrees of freedom (DF) for each source of variation.
|
|
|
Gives the p-value for the test. The Prob > F value measures the probability of obtaining an F Ratio as large as what is observed, given that all parameters except the intercept are zero. Small values of Prob > F indicate that the observed F Ratio is unlikely. Such values are considered evidence that there is at least one significant effect in the model.
|
The Parameter Estimates report shows the estimates of the model parameters and, for each parameter, gives a t test for the hypothesis that it equals zero.
Note: Estimates are obtained and tested, if possible, even when there are linear dependencies among the model terms. Such estimates are labeled Biased or Zeroed. For details, see Models with Linear Dependencies among Model Terms.
|
Gives the model term corresponding to the estimated parameter. The first term is always the intercept, unless the No Intercept option was checked in the Fit Model launch window. Continuous effects appear with the name of the data table column. Note that continuous columns that are part of higher order terms might be centered. Nominal or ordinal effects appear with values of levels in brackets. See Coding for Nominal Effects and the Statistical Details section for information about the coding of nominal and ordinal terms.
|
|
|
t Ratio
|
Tests whether the true value of the parameter is zero. The t Ratio is the ratio of the estimate to its standard error. Given the usual assumptions about the model, the t Ratio has a Student’s t distribution under the null hypothesis.
|
|
Lists the p-value for the test that the true parameter value is zero, against the two-sided alternative that it is not.
|
|
|
where Ri 2 is the RSquare, or coefficient of multiple determination, for the regression of xi as a function of the other explanatory variables.
|
|
|
Shows the square roots of the relative variances of the parameter estimates (Goos and Jones, 2011, p. 25):
|
The Effect Tests report only appears when there are fixed effects in the model. The effect test for a given effect tests the null hypothesis that all parameters associated with that effect are zero. An effect might have only one parameter as for a single continuous explanatory variable. In this case, the test is equivalent to the t test for that term in the Parameter Estimates report. A nominal or ordinal effect can have several associated parameters, based on its number of levels. The effect test for such an effect tests whether all of the associated parameters are zero.
|
•
|
|
•
|
|
Shows the degrees of freedom for the effect test. Ordinarily, Nparm and DF are the same. They can differ if there are linear dependencies among the predictors. In such cases, DF might be less than Nparm, indicating that at least one parameter associated with the effect is not testable. Whenever DF is less than Nparm, the note LostDFs appears to the right of the line in the report. If there are degrees of freedom for error, the test is conducted. For details, see Effect Tests Report.
|
|
|
Gives the F statistic for testing that the effect is zero. The F Ratio is the ratio of the mean square for the effect divided by the mean square for error. The mean square for the effect is the sum of squares for the effect divided by its degrees of freedom.
|
|
|
Gives the p-value for the effect test.
|
|
The red triangle options next to an effect name are described in Description of Effect Options. For certain modeling types, some of these options might not be appropriate and are therefore not available.
|
Gives tests and confidence intervals for pairwise comparisons of least squares means using Student’s t tests. See LSMeans Student’s t and LSMeans Tukey HSD.
Note: The significance level applies to individual comparisons and not to all comparisons collectively. The error rate for the collection of comparisons is greater than the error rate for individual tests.
|
|
|
Gives tests and confidence intervals for pairwise comparisons of least squares means using the Tukey-Kramer HSD (Honestly Significant Difference) test (Tukey 1953, Kramer, 1956). See LSMeans Student’s t and LSMeans Tukey HSD.
|
|
Least squares means are values predicted by the model for the levels of a categorical effect where the other model factors are set to neutral values. The neutral value for a continuous effect is defined to be its sample mean. The neutral value for a nominal effect that is not involved in the effect of interest is the average of the coefficients for that effect. The neutral value for an uninvolved ordinal effect is defined to be the first level of the effect in the value ordering.
Least squares means are also called adjusted means or population marginal means. Least squares means can differ from simple means when there are other effects in the model. In fact, it is common for the least squares means to be closer together than the sample means. This situation occurs because of the nature of the neutral values where these predictions are made.
Because least squares means are predictions at specific values of the other model factors, you can compare them. When effects are tested, comparisons are made using the least squares means. For further details about least squares means, see Least Squares Means across Nominal Factors in Statistical Details and Ordinal Least Squares Means.
For main effects, the Least Squares Means Table also includes the sample mean (Least Squares Mean Table).
|
1.
|
|
2.
|
Select Analyze > Fit Model.
|
|
3.
|
|
4.
|
|
5.
|
|
6.
|
Click Run.
|
The Effect Details report, shown in Least Squares Mean Table, shows reports for each of the three effects. Least Squares Means tables are given for age and sex, but not for the continuous effect height. Notice how the least squares means differ from the sample means.
This option constructs least squares means (LS Means) plots for nominal and ordinal main effects and their interactions. The Popcorn.jmp sample data table illustrates an interaction between two categorical effects. Least Squares Means Tables and Plots for Two Effects shows the Least Squares Means tables and the corresponding LS Means plots for two categorical effects in the Popcorn.jmp sample data table.
To create the report in Least Squares Means Tables and Plots for Two Effects, follow these steps:
|
1.
|
|
2.
|
Select Analyze > Fit Model.
|
|
3.
|
|
4.
|
Select popcorn, oil amt, and batch and click Macros > Full Factorial. Note that the Emphasis changes to Effect Screening.
|
|
5.
|
Click Run.
|
|
7.
|
|
8.
|
To transpose the factors in the plot for popcorn*batch, deselect the LSMeans plot option. Then hold the SHIFT key while you select the LSMeans Plot option again.
|
LSMeans Plot for Interaction with Factors Transposed shows the popcorn*batch interaction plot with the factors transposed. Compare it with the plot in Least Squares Means Tables and Plots for Two Effects. These plots depict the same information but, depending on your interest, one might be more intuitive than the other.
A contrast is a linear combination of parameter values. In the Contrast Specification window, you can specify multiple contrasts and jointly test whether they are zero (LSMeans Contrast Specification for age).
Each time you click the + or - button, the contrast coefficients are normalized to make their sum zero and their absolute sum equal to two, if possible. To compare additional levels, click the New Column button. A new column appears in which you define a new contrast. After you are finished, click Done. The Contrast report appears (LSMeans Contrast Report). The overall test is a joint F test for all contrasts.
p-value for the significance test
The Test Detail report (LSMeans Contrast Report) shows a column for each contrast that you tested. For each contrast, the report gives its estimated value, its standard error, a t ratio for a test of that single contrast, the corresponding p-value, and its sum of squares.
The Parameter Function report (LSMeans Contrast Report) shows the contrasts that you specified expressed as linear combinations of the terms of the model.
|
1.
|
|
2.
|
Select Analyze > Fit Model.
|
|
3.
|
|
4.
|
|
5.
|
Select age in the Select Columns list, select height in the Construct Model Effects list, and click Cross.
|
|
6.
|
Click Run.
|
|
7.
|
|
10.
|
Note that there is a text box next to the continuous effect height. The default value is the mean of the continuous effect.
|
|
11.
|
Click Done.
|
The Contrast report is shown in LSMeans Contrast Report. The test for the contrast is significant at the 0.05 level. You conclude that the predicted weight for age 12 and 13 children differs statistically from the predicted weight for age 14 and 15 children at the mean height of 62.55.
The LSMeans Student’s t and LSMeans Tukey HSD (honestly significant difference) options test pairwise comparisons of model effects.
|
•
|
The LSMeans Student’s t option is based on the usual independent samples, equal variance t test. Each comparison is based on the specified significance level. The overall error rate resulting from conducting multiple comparisons exceeds that specified significance level.
|
LSMeans Tukey HSD Report shows the LSMeans Tukey report for the effect age in the Big Class.jmp sample data table. (You can obtain this report by running the Fit Model data table script and selecting LS Means Tukey HSD from the red triangle menu for age.) By default, the report shows the Crosstab Report and the Connecting Letters Report.
In LSMeans Tukey HSD Report, levels 17, 12, 16, 13, and 15 are connected by the letter A. The connection indicates that these levels do not differ at the 0.05 significance level. Also, levels 16, 13, 15, and 14 are connected by the letter B, indicating that they do not differ statistically. However, ages 17 and 14, and ages 12 and 14, are not connected by a common letter, indicating that these two pairs of levels are statistically different.
Bar Chart from LSMeans Differences HSD Connecting Letters Table shows the bar chart for an example based on Big Class.jmp. Run the Fit Model data table script, select LSMeans Tukey HSD from the red triangle menu for age. Select Save Connecting Letters Table from the LSMeans Differences Tukey HSD report. Run the Bar Chart script in the data table that appears.
Ranks the differences from largest to smallest, giving standard errors, confidence limits, and p-values. Also plots the differences on a bar chart with overlaid confidence intervals.
Gives individual detailed reports for each comparison. For a given comparison, the report shows the estimated difference, standard error, confidence interval, t ratio, degrees of freedom, and p-values for one- and two-sided tests. Also shown is a plot of the t distribution, which illustrates the significance test for the comparison. The area of the shaded portion is the p-value for a two-sided test.
Uses the Two One-Sided Tests (TOST) method to test for a practical difference between the means (Schuirmann, 1987). You must select a threshold difference for which smaller differences are considered practically equivalent. Two one-sided t tests are constructed for the null hypotheses that the true difference exceeds the threshold values. If both tests reject, this indicates that the difference in the means does not exceed either threshold value. Therefore, the groups are considered practically equivalent.
A report for the LSMeans Dunnett option for effect treatment in the Cholesterol.jmp sample data table is shown in LSMeans Dunnett Report. Here, the response is June PM and the level of treatment called Control is specified as the control level.
The Test Slice reports follow the same format as do the LSMeans Contrast reports. See LSMeans Contrast.
Opens the Power Details window, where you can enter information to obtain retrospective or prospective details for the F test of a specific effect.
Note: To ensure that your study includes sufficiently many observations to detect the required differences, use information about power when you design your experiment. Such an analysis is called a prospective power analysis. Consider using the DOE platform to design your study. Both DOE > Sample Size and Power and DOE > Evaluate Design are useful for prospective power analysis. For an example of a prospective power analysis using standard least squares, see Prospective Power Analysis.
Power Details Window shows an example of the Power Details window for the Big Class.jmp sample data table. Using the Power Details window, you can explore power for values of alpha ( ), sigma (
), sigma ( ), delta (
), delta ( ), and Number (study size). Enter a single value (From only), two values (From and To), or the start (From), stop (To), and increment (By) for a sequence of values. Power calculations are reported for all possible combinations of the values that you specify.
), and Number (study size). Enter a single value (From only), two values (From and To), or the start (From), stop (To), and increment (By) for a sequence of values. Power calculations are reported for all possible combinations of the values that you specify.
|
Alpha (α)
|
|
|
Sigma (σ)
|
|
|
Delta (δ)
|
The effect size of interest. See Effect Size for details. The initial value, shown in the first row, is the square root of the sum of squares for the hypothesis divided by the number of observations in the study.
|
|
Number (n)
|
|
|
Solves for the power as a function of α, σ, δ, and n. The power is the probability of detecting a difference of size δ by seeing a test result that is significant at level α, for the specified σ and n. For more details, see Computations for the Power in Statistical Details.
|
|
|
Solves for the smallest number of observations required to obtain a test result that is significant at level α, for the specified δ and σ. For more details, see Computations for the LSN in Statistical Details.
|
|
|
Solves for the smallest positive value of a parameter or linear function of the parameters that produces a p-value of α. The least significant value is a function of α, σ, and n. This option is available only for one-degree-of-freedom tests. For more details, see Computations for the LSV in Statistical Details.
|
|
|
Retrospective power calculations use estimates of the standard error and the test parameters in estimating the F distribution’s noncentrality parameter. Adjusted power is retrospective power calculation based on an estimate of the noncentrality parameter from which positive bias has been removed (Wright and O’Brien, 1988).
The adjusted power deals with a sample estimate, so it and its confidence limits are computed only for the δ estimated in the current study. For more details, see Computations for the Adjusted Power in Statistical Details.
|
The Lack of Fit report gives details for a test that assesses whether the model fits the data well. The Lack of Fit report only appears when it is possible to conduct this test. The test relies on the ability to estimate the variance of the response using an estimate that is independent of the model. Constructing this estimate requires that response values are available at replicated values of the model effects. The test involves computing an estimate of pure error, based on a sum of squares, using these replicated observations.
|
•
|
There are no replicated points with respect to the X variables, so it is impossible to calculate a pure error sum of squares.
|
|
•
|
The model is saturated, meaning that there are as many estimated parameters as there are observations. Such a model fits perfectly, so it is impossible to assess lack of fit.
|
The difference between the error sum of squares from the model and the pure error sum of squares is called the lack of fit sum of squares. The lack of fit variation can be significantly greater than pure error variation if the model is not adequate. For example, you might have the wrong functional form for a predictor, or you might not have enough, or the correct, interaction effects in your model.
|
|||||
where SSi is the sum of the squared differences between each observed response and the mean response for the ith group.
|
|||||
|
Shows the ratio of the Mean Square for Lack of Fit to the Mean Square for Pure Error. The F Ratio tests the hypothesis that the variances estimated by the Lack of Fit and Pure Error mean squares are equal, which is interpreted as representing “no lack of fit”.
|
|||||