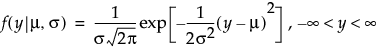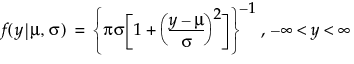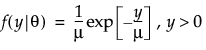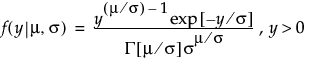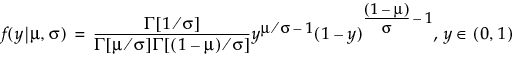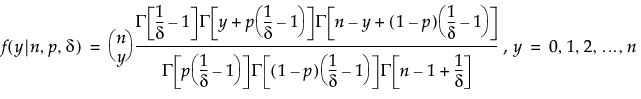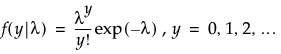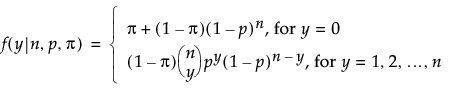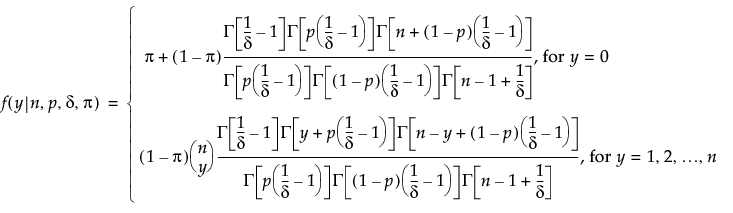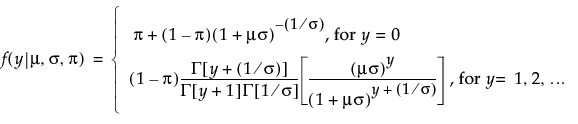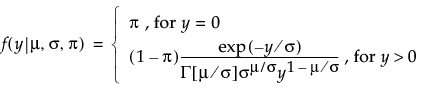An l2 penalty is applied to the regression coefficients during ridge regression. Ridge regression coefficient estimates are given by the following:
,
is the l2 penalty, λ is the tuning parameter, N is the number of rows, and p is the number of variables.An l1 penalty is applied to the regression coefficients during Lasso. Coefficient estimates for the Lasso are given by the following:
,
is the l1 penalty, λ is the tuning parameter, N is the number of rows, and p is the number of variablesThe Elastic Net combines both l1 and l2 penalties. Coefficient estimates for the Elastic Net are given by the following:
,|
•
|
is the |
•
|
is the |
•
|
λ is the tuning parameter
|
|
•
|
|
•
|
N is the number of rows
|
|
•
|
p is the number of variables
|
The adaptive Lasso method uses weighted penalties to provide consistent estimates of coefficients. The weighted form of the l1 penalty is
,
is the MLE when the MLE exists. If the MLE does not exist and the response distribution is normal, estimation is done using least squares and 
is the solution obtained using a generalized inverse. If the response distribution is not normal, 
is the ridge solution.For the adaptive Lasso, this weighted form of the l1 penalty is used in determining the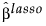 
coefficients.
coefficients.The adaptive Elastic Net uses this weighted form of the l1 penalty and also imposes a weighted form of the l2 penalty. The weighted form of the l2 penalty for the adaptive Elastic Net is
,
is the MLE when the MLE exists. If the MLE does not exist and the response distribution is normal, estimation is done using least squares and 
is the solution obtained using a generalized inverse. If the response distribution is not normal, 
is the ridge solution.The lower bound is zero except in special cases where it is set to 0.01. See Tuning Parameter. When the lower bound for the tuning parameter is zero, the solution is unpenalized and the coefficients are the MLEs. The upper bound is the smallest value for which all of the non-intercept terms are zero.
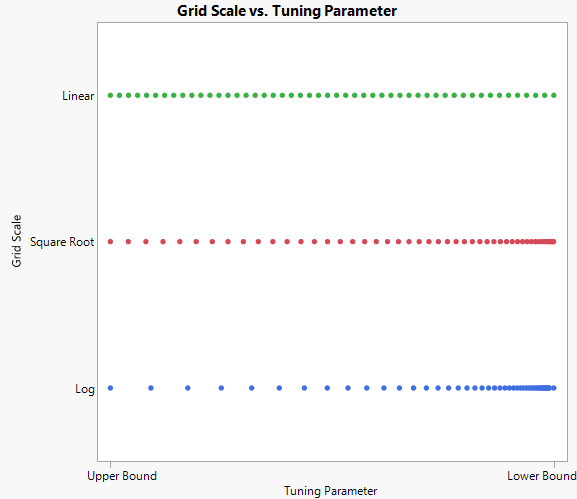
In some cases, there is a large gap between the unpenalized estimates and the previous step. This large gap can distort the solution path. The log scale focuses its search on small tuning parameter values with few large values, whereas the linear scale evenly disperses the search from the minimum to the maximum value. The square root scale is a compromise between the other two scales. Options for Tuning Parameter Grid Scale shows the different grid scales.
