One approach to comparing two means is to determine whether their actual difference is greater than their least significant difference (LSD). This least significant difference is a Student’s t-statistic multiplied by the standard error of the difference of the two means and is written as follows:
These squared values form a Pythagorean relationship, illustrated graphically by the right triangle shown in Relationship of the Difference between Two Means.
Geometric Relationship of t-test Statistics
|
•
|
If the circles intersect so that the outside angle is greater than a right angle, then the means are not significantly different. If the circles intersect so that the outside angle is less than a right angle, then the means are significantly different. An outside angle of less than 90 degrees indicates that the means are farther apart than the least significant difference.
|
|
•
|
To compute power, you make use of the noncentral F distribution. The formula (O’Brien and Lohr 1984) is given as follows:
|
•
|
F is distributed as the noncentral
|
|
•
|
|
•
|
|
•
|
n is the number per group.
|
|
•
|
r is the number of groups.
|
|
•
|
|
•
|
|
•
|
μ is the overall mean.
|
|
•
|
σ2 is estimated by the mean squared error (MSE).
|
Using quantities from the Analysis of Variance report for the model, the R2 for any continuous response fit is always calculated as follows:
The mean square for Error is found in the Analysis of Variance report and the mean square for C. Total can be computed as the C. Total Sum of Squares divided by its respective degrees of freedom. See The Analysis of Variance Report.
Brown-Forsythe is the model F statistic from an ANOVA on  where
where  is the median response for the ith level.
is the median response for the ith level.
The Levene F is the model F statistic from an ANOVA on  where
where  is the mean response for the ith level.
is the mean response for the ith level.
and ni is the count on the ith level and si2 is the response sample variance on the ith level. The Bartlett statistic has a χ2-distribution. Dividing the Chi-square test statistic by the degrees of freedom results in the reported F value.
and ni is the count on the ith level,  is the mean response for the ith level, and si2 is the response sample variance for the ith level.
is the mean response for the ith level, and si2 is the response sample variance for the ith level.


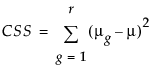 is the corrected sum of squares.
is the corrected sum of squares.
 where
where 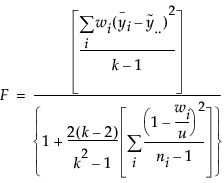 where
where  ,
,  ,
,