With the exception of the Crow-AMSAA with Modified MLE option, the estimates for λ and β are maximum likelihood estimates, computed as follows. The likelihood function is derived using the methodology in Meeker and Escobar (1998). It is reparametrized in terms of param1 = log(λ) and param2 = log(β). This is done to enable the use of an unconstrained optimization algorithm, namely, an algorithm that searches from - to +
to +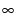 . The MLEs for param1 and param2 are obtained.
. The MLEs for param1 and param2 are obtained.
The standard errors for λ and β are obtained from the Fisher information matrix. Confidence limits for param1 and param2 are calculated based on the asymptotic distribution of the MLEs, using the Wald statistic. These estimates and their confidence limits are then transformed back to the original units using the exponential function.
For the Crow AMSAA with Modified MLE option, the estimate for β is corrected for bias. The formula for the bias-corrected estimate of β depends on whether the test is failure terminated or time terminated.
The modified MLE for λ, denoted λ, is calculated according to the expression given by the likelihood function, but based on the adjusted value of beta:
The covariance matrix for the parameters is estimated using the Fisher information matrix (see Parameter Estimates for Crow-AMSAA Models). However, the bias-corrected estimates for λ and β are substituted for the MLEs in the resulting formulas. All confidence bands in plots and confidence intervals in reports are based on this procedure.
For the Crow-AMSAA models, the estimates for the MTBF, Intensity, and Cumulative Events given in the profilers are obtained by replacing the parameters λ and β in their theoretical expressions by their MLEs. In the case of the Crow-AMSAA with Modified MLE option, the modified MLEs are used. Confidence limits are obtained by applying the delta method to the log of the expression of interest.
For example, consider the cumulative events function. The cumulative number of events at time t since testing initiation is given by N(t) = λtβ. It follows that log(N(t)) = log(λ) + βlog(t). The parameters λ and β in log(N(t)) are replaced by their MLEs (or modified MLEs) to estimate log(N(t)). The delta method is applied to this expression to obtain an estimate of its variance. This estimate is used to construct a 95% Wald-based confidence interval. The resulting confidence limits are then transformed using the exponential function to give confidence limits for the estimated cumulative number of events at time t.
 for a failure-terminated test
for a failure-terminated test for a time-terminated test
for a time-terminated test