Shows the overlaid failure plots (proportion failing over time) for each group (in the tradition of the reliability literature.) A failure plot reverses the y-axis to show the number of failures rather than the number of survivors.
Note: The first seven options (Show Points, Show Kaplan Meier, Show Combined, Show Confid Interval, Show Simultaneous CI, Show Shaded Pointwise CI, and Show Shaded Simultaneous CI) and the last two options (Fitted Survival CI, Fitted Failure CI) pertain to the initial survival plot and failure plot. The other five (Midstep Quantile Points, Connect Quantile Points, Fitted Quantile, Fitted Quantile CI Lines, Fitted Quantile CI Shaded) pertain only to the distributional plots.
|
‒
|
Show Points shows the sample points at each step of the survival plot. Failures appear at the bottom of the steps, and censorings are indicated by points above the steps.
|
|
‒
|
Show Kaplan Meier shows the Kaplan-Meier curves. This option is on by default.
|
|
‒
|
Show Combined shows the survival curve for the combined groups in the Survival Plot.
|
|
‒
|
Show Confid Interval shows the pointwise 95% confidence bands on the survival plot for groups and for the combined plot when it appears with the Show Combined option.
|
|
‒
|
When you select Show Points and Show Combined, the survival plot for the total or combined sample appears as a gray line. The points also appear at the plot steps of each group.
|
|
‒
|
Show Simultaneous CI shows the simultaneous confidence bands for all groups on the plot. Meeker and Escobar (1998, chap. 3) discuss pointwise and simultaneous confidence intervals and the motivation for simultaneous confidence intervals in survival analysis.
|
|
‒
|
Midstep Quantile Points changes the plotting positions to use the modified Kaplan-Meier plotting positions, which are equivalent to taking mid-step positions of the Kaplan-Meier curve, rather than the bottom-of-step positions. This option is recommended, so it is on by default.
|
|
‒
|
Connect Quantile Points shows the lines in the plot. This option is on by default.
|
|
‒
|
Fitted Quantile shows the straight-line fit on the fitted Weibull, lognormal, or exponential plot. This option is on by default.
|
|
‒
|
Fitted Quantile CI Lines shows the 95% confidence bands for the fitted Weibull, lognormal, or exponential plot.
|
|
‒
|
Fitted Quantile CI Shaded shows the display of the 95% confidence bands for a fit as a shaded area or dashed lines.
|
|
‒
|
Fitted Survival CI shows the confidence intervals (on the survival plot) of the fitted distribution.
|
|
‒
|
Fitted Failure CI shows the confidence intervals (on the failure plot) of the fitted distribution.
|
Plots the cumulative exponential failure probability by time for each group. Lines that are approximately linear empirically indicate the appropriateness of using an exponential model for further analysis. For example, in Exponential, Weibull, and Lognormal Plots and Reports, the lines for Group 1 and Group 2 in the Exponential Plot are curved rather than straight. This indicates that the exponential distribution is not appropriate for this data. See Exponential, Weibull, and Lognormal Plots and Fits.
Produces the Exponential Parameters table and the linear fit to the exponential cumulative distribution function in the Exponential Plot. See Exponential, Weibull, and Lognormal Plots and Reports. The parameter Theta corresponds to the mean failure time. See Exponential, Weibull, and Lognormal Plots and Fits.
Plots the cumulative Weibull failure probability by log(time) for each group. A Weibull plot that has approximately parallel and straight lines indicates a Weibull survival distribution model might be appropriate to use for further analysis. See Exponential, Weibull, and Lognormal Plots and Fits.
Produces the linear fit to the Weibull cumulative distribution function in the Weibull plot and two popular forms of Weibull estimates. These estimates are shown in the Extreme-value Parameter Estimates table and the Weibull Parameter Estimates tables. See Exponential, Weibull, and Lognormal Plots and Reports. The Alpha parameter is the 0.632 quantile of the failure-time distribution. The Extreme-value table shows a different parameterization of the same fit, where Lambda = ln(Alpha) and Delta = 1/Beta. See Exponential, Weibull, and Lognormal Plots and Fits.
Plots the cumulative lognormal failure probability by log(time) for each group. A lognormal plot that has approximately parallel and straight lines indicates a lognormal distribution is appropriate to use for further analysis. See Exponential, Weibull, and Lognormal Plots and Fits.
Produces the linear fit to the lognormal cumulative distribution function in the lognormal plot and the LogNormal Parameter Estimates table shown in Exponential, Weibull, and Lognormal Plots and Reports. Mu and Sigma correspond to the mean and standard deviation of a normally distributed natural logarithm of the time variable. See Exponential, Weibull, and Lognormal Plots and Fits.
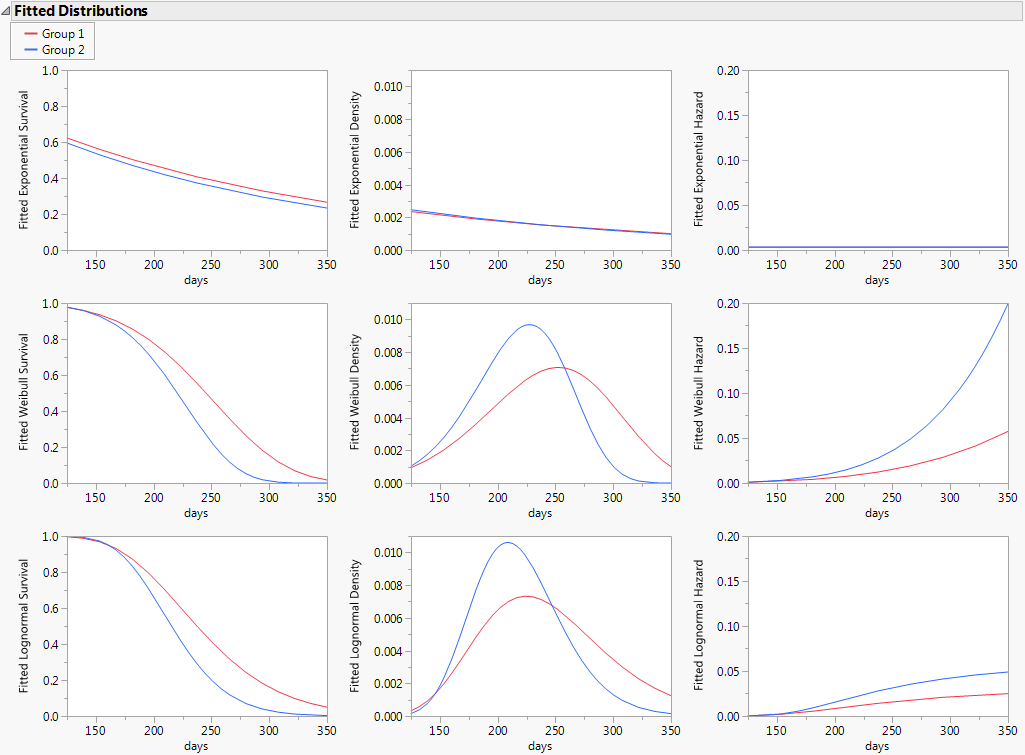
Use in conjunction with the fit options to show three plots corresponding to the fitted distributions: Survival, Density, and Hazard. If you have not performed a fit, no plot appears. See Fitted Distribution Plots.
Performs an estimation of the Weibull model using the specified causes to indicate a failure event and other causes to indicate censoring. The fitted distribution appears as a dashed line in the Survival Plot. See Competing Causes.
The Weibull distribution is the most popular for event-time data. There are many ways in which different authors parameterize this distribution (as shown in Various Weibull Parameters in Terms of JMP’s alpha and beta). JMP reports two parameterizations, labeled the lambda-delta extreme value parameterization and the Weibull alpha-beta parameterization. The alpha-beta parameterization is used in the reliability literature. See Nelson (1990). Alpha is interpreted as the quantile at which 63.2% of the units fail. Beta is interpreted as follows: if beta>1, the hazard rate increases with time; if beta<1, the hazard rate decreases with time; and if beta=1, the hazard rate is constant, meaning it is the exponential distribution.
|
alpha=alpha
|
beta=beta
|
|
|
eta=alpha
|
beta=beta
|
|
|
c = alpha
|
m = beta
|
|
|
eta=alpha
|
beta=beta
|
|
|
exp(X beta)=alpha
|
lambda=beta
|
|
|
beta=alpha
|
alpha=beta
|
|
|
lambda = 1/alpha
|
p = beta
|
|
|
lambda=log(alpha)
|
delta=1/beta
|
|
|
mu=log(alpha)
|
sigma=1/beta
|
The lognormal distribution is also very popular. This is the distribution where if you take the log of the values, the distribution is normal. If you want to fit data to a normal distribution, you can take the exp() of it and analyze it as lognormal. See Additional Examples of Fitting Parametric Survival in Fit Parametric Survival.
To see additional options for the exponential, Weibull, and lognormal fits, hold down the Shift key, click the red triangle of the Product-Limit Survival Fit menu, and click on the desired fit.
|
•
|
|
•
|
JMP can constrain the values of the Theta (Exponential), Beta (Weibull), and Sigma (LogNormal) parameters when fitting these distributions. This feature is needed in WeiBayes situations, for example:
These plots can be transferred to other graphs through the use of graphic scripts. To copy the graph, right-click in the plot to be copied and select Edit > Copy Frame Contents. Right-click in the destination plot and select Edit > Paste Frame Contents.
Adds a new column to the current table called log(–log(Surv)). This information is often used to plot against the time variable with a grouping variable, such as the code for type of failure.