The Time Series platform begins by showing a time series plot, like the one shown previously in Time Series Plot of Seriesg (Airline Passenger) Data. The Graph command on the platform popup menu has a submenu of controls for the time series plot with the following commands.
|
•
|
For autocorrelation, the Ljung-Box Q and p-values appear for each lag. The Q-statistic can be used to test whether a group of autocorrelations is significantly different from zero, or to test that the residuals from a model can be distinguished from white noise.
|
|
•
|
The number of lags begins with 0 to provide a broader picture of the analysis. To compute correlations beginning with lag 1, modify the JMP preferences before generating the graph. Select File > Preferences > Platforms > Time Series and then select Suppress Lag 0 in ACF and PACF.
|
The autocorrelation for the kth lag is computed as follows:
where 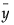 is the mean of the N non-missing points in the time series. The bars graphically depict the autocorrelations.
is the mean of the N non-missing points in the time series. The bars graphically depict the autocorrelations.
By definition, the first autocorrelation (lag 0) always has length 1. The curves show twice the large-lag standard error (± 2 standard errors), computed as
For partial autocorrelation, the blue lines represent ± 2 standard errors for approximate 95% confidence limits, where the standard error is computed as follows:
The Variogram command alternately displays or hides the graph of the variogram. The variogram measures the variance of the differences of points k lags apart and compares it to that for points one lag apart. The variogram is computed from the autocorrelations as
where rk is the autocorrelation at lag k. The plot on the left in Variogram Graph (left) and AR Coefficient Graph (right) shows the Variogram graph for the Seriesg data.
The AR Coefficients command alternately displays or hides the graph of the least squares estimates of the autoregressive (AR) coefficients. The definition of these coefficients is given below. These coefficients approximate those that you would obtain from fitting a high-order, purely autoregressive model. The right-hand graph in Variogram Graph (left) and AR Coefficient Graph (right) shows the AR coefficients for the Seriesg data.
The Spectral Density command alternately displays or hides the graphs of the spectral density as a function of period and frequency (Spectral Density Plots).
The periodogram is smoothed and scaled by 1/(4π) to form the spectral density.
The Fisher’s Kappa statistic tests the null hypothesis that the values in the series are drawn from a normal distribution with variance 1 against the alternative hypothesis that the series has some periodic component. Kappa is the ratio of the maximum value of the periodogram, I(fi), and its average value. The probability of observing a larger Kappa if the null hypothesis is true is given by
where q = N / 2 if N is even, q = (N - 1) / 2 if N is odd, and κ is the observed value of Kappa. The null hypothesis is rejected if this probability is less than the significance level α.
For q - 1 > 100, Bartlett’s Kolmogorov-Smirnov compares the normalized cumulative periodogram to the cumulative distribution function of the uniform distribution on the interval (0, 1). The test statistic equals the maximum absolute difference of the cumulative periodogram and the uniform CDF. If it exceeds 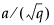 , then reject the hypothesis that the series comes from a normal distribution. The values a = 1.36 and a = 1.63 correspond to significance levels 5% and 1% respectively.
, then reject the hypothesis that the series comes from a normal distribution. The values a = 1.36 and a = 1.63 correspond to significance levels 5% and 1% respectively.
Save Spectral Density creates a new table containing the spectral density and periodogram where the (i+1)th row corresponds to the frequency fi = i / N (that is, the ith harmonic of 1 / N).
The Difference command computes the differenced series and produces graphs of the autocorrelations and partial autocorrelations of the differenced series. These graphs can be used to determine whether the differenced series is stationary.
Several of the time series models described in the next sections accommodate a differencing operation (the ARIMA, Seasonal ARIMA models, and some of the smoothing models). The Difference command is useful for determining the order of differencing that should be specified in these models.
The Differencing Specification dialog appears in the report window when you select the Difference command. It enables you to specify the differencing operation that you want to apply to the time series. Click Estimate to see the results of the differencing operation. The Specify Differencing dialog enables you to specify the Nonseasonal Differencing Order, d, the Seasonal Differencing Order, D, and the number of Periods Per Season, s. Selecting zero for the value of the differencing order is equivalent to no differencing of that kind.
controls the plot of the differenced series and behaves the same as those under the Time Series Graph menu.
appends the differenced series to the original data table. The leading d + sD elements are lost in the differencing process. They are represented as missing values in the saved series.
Removes the linear trend from the data, where Trend = β0 + β1 time. A Time Series report for the detrended series is added to the report window. Also, a column containing the most recently detrended series is added to the data table.
Note: When you select the Remove Linear Trend option, JMP adds a column to the data table that contains the detrended data. If this column is already present in the data table when the option is selected, JMP overwrites the existing column.
Removes cyclical effects from the data. You can specify the number of units per cycle and indicate whether a constant should be subtracted from the data. A Time Series report for the decycled series is added to the report window. Also, a column containing the most recently decycled series is added to the data table. See Remove Cycle.
Note: When you select the Remove Cycle option, JMP adds a column to the data table that contains the decycled data. If this column is already present in the data table when the option is selected, JMP overwrites the existing column.
Removes trend and seasonal effects using the X-11 method developed by the US Bureau of the Census (Shiskin et. al., 1967). Available only for monthly or quarterly data. You can specify a multiplicative or additive X-11 adjustment. See X11.
|
•
|
C is the (optional) Constant.
|
|
•
|
A is the Amplitude of the cosine wave.
|
|
•
|
U is the number of Units per Cycle.
|
|
•
|
P is the Phase of the cosine wave.
|
|
•
|
t is one less than the row number of a given observation.
|
When regarded as number of seconds since January 1, 1904, the data in the X, Time ID column must represent exact monthly or quarterly increments. This is best accomplished by using a Time ID column that has a Date Format of m/y or yyyyQq. (See Using JMP for information about Date Formats.)
This method adjusts the original time series using either a multiplicative or an additive decomposition. The model is fit using an iterative process to estimate the three X-11 components: trend cycle, seasonal, and irregular. The trend cycle component contains both the long-term trend and the long-term cyclical effects. The irregular component contains the effects of variation unexplained by the trend and seasonal components. For a historical overview of the development of the X-11 method, see SAS/ETS 13.1 User’s Guide (search for “Historical Development of X-11”).
Ot is the original time series
Ct is the trend cycle component
St is the seasonal component
It is the irregular component
Overlays the X11-adjusted time series on the original time series, Ot. Original and Adjusted Plot for X11 Analysis for Monthly Sales.jmp shows an example of the original and adjusted time series plot. The X11-adjusted values are 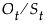 for the multiplicative adjustment and
for the multiplicative adjustment and 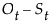 for the additive adjustment.
for the additive adjustment.
Shows or hides the X11 summary tables, as described in Shiskin et. al. (1967). The tables are grouped into five categories (labeled B through F), described in Descriptions of the Categories of X11 Output Tables.
Saves four columns to the data table: the seasonally adjusted time series, the seasonal components (St), the trend cycle components (Ct), and the irregular series components (It).
Saves columns to the data table for all of the tables produced in the report by the Show Tables option.
For details about the contents of the X11 output tables, see Shisken et. al. (1967) or SAS/ETS 13.1 User’s Guide (search for “The output from PROC X11”).
The plot show how an observation at time t is related to another observation at time t +/- p. +/- p is the lag, because the plot allows negative values and positive values.
The Number of Forecast Periods command displays a dialog for you to reset the number of periods into the future that the fitted models will forecast. The initial value is set in the Time Series Launch dialog. All existing and future forecast results will show the new number of periods with this command.

 where
where 









