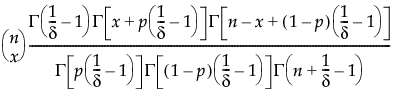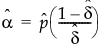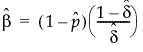Poisson 分布只有一个尺度参数 λ > 0。
pmf: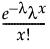 
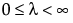; x = 0,1,2,...
; x = 0,1,2,...Gamma Poisson 分布的假设前提是：x|μ 服从 Poisson 分布，μ 服从 Gamma(α,τ) 分布。Gamma Poisson 包含参数 λ = ατ 和 σ = τ+1。参数 σ 是一个离散参数。若 σ > 1，则出现过度离散，这意味着 x 的变异比 Poisson 分布本身所解释的要大。若 σ = 1，x 将简化为 Poisson(λ)。
pmf: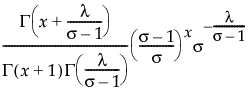 
; 
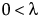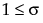; x = 0,1,2,...
; ; x = 0,1,2,...
是 Gamma 函数。
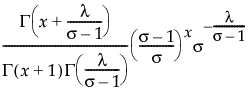
是 若 α 的估计值为整数，则 Gamma Poisson 等价于负二项分布，pmf 如下：
（ 
）运行 JMP Samples/Scripts 文件夹中的 demoGammaPoisson.jsl，比较带有参数 λ 和 σ 的 Gamma Poisson 分布与带有参数 λ 的 Poisson 分布。
二项选项接受两种格式的数据：常数样本大小或包含样本大小的列。
; Beta 二项分布的假设前提是：x|π 服从 Binomial(n,π) 分布，π 服从 Beta(α,β) 分布。Beta 二项分布具有参数 p = α/(α+β) 和 δ = 1/(α+β+1)。参数 δ 是一个离散参数。若 δ > 0，则出现过度离散，这意味着 x 的变异比二项分布本身所解释的要大。若 δ < 0，则出现离散不足。若 δ = 0，x 呈 Binomial(n,p) 分布。仅当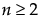 
才存在 Beta 二项分布。
才存在 Beta 二项分布。
; 
; 
是 Gamma 函数。请记住 x|π ~ Binomial(n,π)，同时 π ~ Beta(α,β)。参数 p = α/(α+β) 和 δ = 1/(α+β+1) 由该平台估计得出。要得到 α 和 β 的估计值，请使用以下公式：
是 p 的估计值。