Receiver Operating Characteristics (ROC) Curves

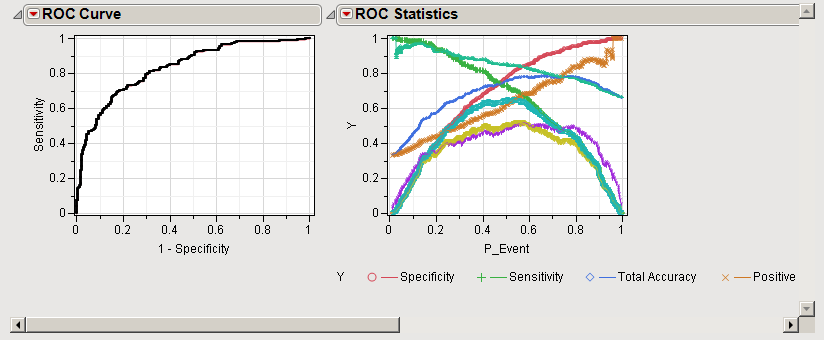
In predictive modeling of a binary response, two parameters, sensitivity , which is the ability to correctly identify those cases with the condition (in this case, disease ), and specificity , which is the ability to correctly identify those without the condition (in this case, healthy ) are plotted against each other and the resulting plot is used to assess how well a test can discriminate between two possibilities across a range of cutoff values. In practice, sensitivity and specificity are diametrically opposed. As the cutoff used to identify positive cases is made more rigorous, thus increasing the probability that cases identified as positive are really positive, the probability of excluding positive cases from the negative cohort goes down. In other words, increased sensitivity results in decreased specificity. These parameters are used to generate a pair of curves displaying Receiver Operating Characteristic ( ROC ) statistics.

The ROC Curve ( left ) plots the increase in sensitivity versus the decrease in specificity at increasingly rigorous cutoff values. The more accurate the classification method used is, the closer the curve approaches the upper left corner of the plot.

Note : As a general rule, 1 - specificity is plotted on the x -axis. This is done so that zero value for each parameter is located at the origin and the plot curves up and to the right.

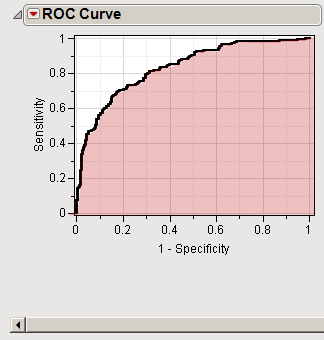
To provide a quantitative measure of the ability of the test to discriminate between the two options, we compute the area under the curve ( AUC ). The AUC corresponds to the pink-shaded region in the figure below.

Because this plot is contained in a one-by-one block, the AUC value is always between zero and one. The closer this area is to one, the better the test is performing across the entire range of specificity and sensitivity values.

Note : An AUC of 0.5 indicates the test is no better than random. An AUC < 0.5 indicates that random assignation of cases to one or the other of the conditions is actually more likely to be correct than your test. If you should ever see this result, something is amiss!

Unfortunately, although a ROC curve can tell you about the trade-off between sensitivity and specificity in your test at different cutoff values, it really does not tell you what cutoff should be used for optimal performance of your test. Additional statistics are needed.

The ROC Statistics plot ( top right ) displays a variety of different statistics across the P-Event , which is the predicted (posterior) probability of an event occurring and is a function of the full range of all of the predictors used in the selected model (plotted along the x -axis). The y -axis on this graph is generic and indexes the individual statistic being considered. Statistics shown here include the following:

•	Sensitivity - the ability to correctly identify those cases with the condition

•	Specificity - the ability to correctly identify those cases that do not have the condition

•	Total Accuracy - the proportion of cases in which the test is able to correctly differentiate between the two outcomes

•	Positive Predictive Value - the proportion of cases with the condition that are correctly identified as having the condition

•	Negative Predictive Value - the proportion of cases without the condition that are correctly identified as not having the condition

•	Matthews Correlation Coefficient - the correlation between the observed and predicted binary predictions

•	Youden Index - equals Sensitivity + Specificity - 1; a measure of distance between the ROC curve at the selected cutoff and the 45 degree line

•	Zero-One Index - the distance between the ROC curve at the selected cutoff and the upper left corner (0,1) point

There is typically no simple way of determining the optimal cutoff for P-Event or which statistic you should use. You must determine which statistics are most appropriate for determining an optimal cutoff for your specific problem. As you examine the different plots, you should consider the relative benefit of making a correct call versus the cost or loss of making an incorrect one.