The
Population Measures
process creates a symmetric matrix
of dissimilarities between specified groups within a study.
Genetic distance
computation is based on differences in group
allele
frequencies calculated using PROC ALLELE for each
marker variable
. Groups are determined by the input values of the specified
population
variable. Multiple genetic distance matrices can be output for separate sets of marker variables if an annotation
By Group
variable is specified.
This process also produces Wright's
F
statistics (Wright, 1951) measuring the degree of relatedness between different types of allele pairs. Cockerham (1969, 1973) defines these same quantities in an analysis of variance (
ANOVA
) framework. For a population hierarchy defined by the Population Variable, the measures computed as Pop Theta, Within Pop f, and Overall F correspond to Wright's F
_ST
, and, when HWE is not assumed, F
_IS
and F
_IT
. A weighted average of these measures over all loci is also reported as an overall estimate as well as measures for individual loci are reported. The estimates of these parameters are calculated using an ANOVA structure along with a method-of-moments approach.
One data set is required to run the
Population Measures
process. This
Input Data Set
, contains all of the marker data.
The
hapmap_subset.sas7bdat
data set used in the following example was generated from data downloaded from the HapMap project (
http://hapmap.ncbi.nlm.nih.gov/
), as follows. Unzipped
.txt
files containing
SNP
data from
chromosome
21, NCBI Build 35, of individuals from four different populations (Utah residents with ancestry from northern and western Europe (CEU), Han Chinese residents of Beijing (HCB), Japanese residents of Tokyo (JPT), and members of the Yoruba group in Ibadan, Nigeria (YRI)) were imported using the
HapMap Input Engine
. The resulting SAS data sets were appended and then filtered to remove related individuals using
pedigree
information provided by the HapMap project (
ftp://ftp.ncbi.nlm.nih.gov/hapmap/samples_individuals/
). The resulting data set was subjected to both the
Marker Properties
and
Subset and Reorder Genetic Data
processes to eliminate low quality (as defined by low MAFs and low Call Rates) SNPs. Finally, 500 markers were selected at random to generate the
hapmap_subset.sas7bdat
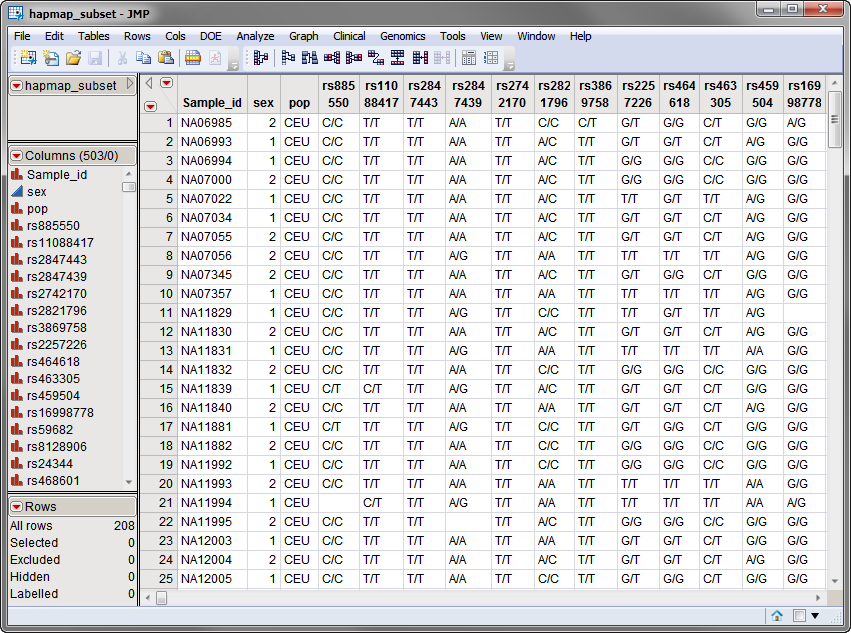
data set. This data set consists of 208 rows of individuals with 500 columns corresponding to SNP marker data on these individuals. Marker data is presented in the one-column genotypic format with delimited alleles. This data set is partially shown below.
Note
:
The
hapmap_subset.sas7bdat
data set is a wide data set; markers are listed in columns, whereas individuals are listed in rows.
A second, optional, data set that can be used in this process
is the
Annotation Data Set
. This data set contains information, such as gene identity or chromosomal location, for each of the markers.
For detailed information about the files and data sets used or created by JMP Life Sciences software, see
Files and Data Sets
.
The output of this process includes three output data sets, two plots, and a set of
Action Buttons
. The data sets and plots are accessed from a tabbed
Results
window.
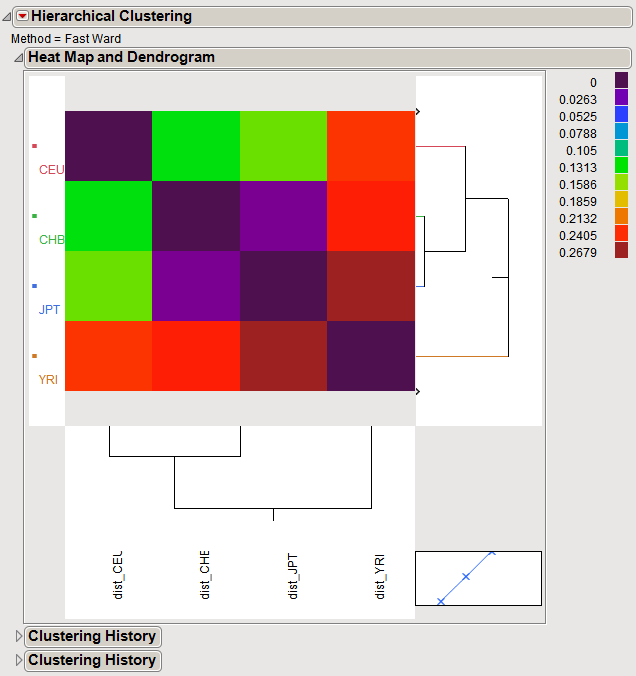
A
Heat Map and Dendrogram
showing the
hierarchical clustering
of the genetic distances calculated in this process is shown below.
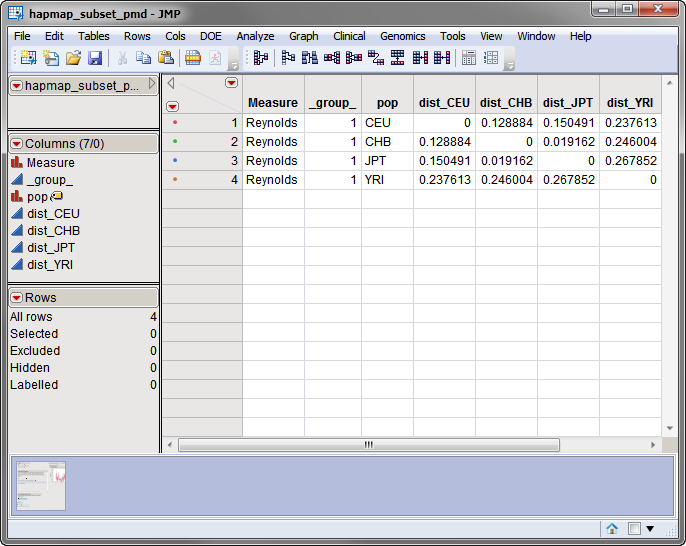
The
hapmap_subset_pmd.sas7bdat
matrix (shown below), used to generate this heat map, is suitable for further analyses. Use the action button to load the output matrix directly into the
Multidimensional Scaling
process.
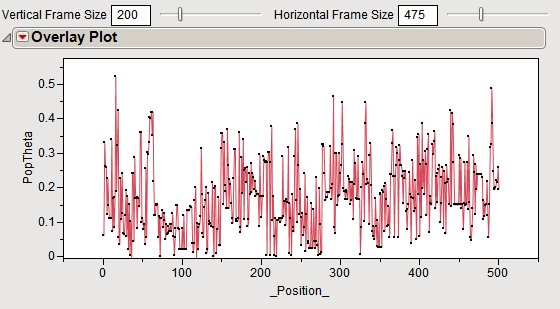
Finally, two output data sets (not shown), listing individual and overall
F-statistics, are generated. The results across the region spanned by the markers, are displayed in the
Overlay Plot
shown below.