A
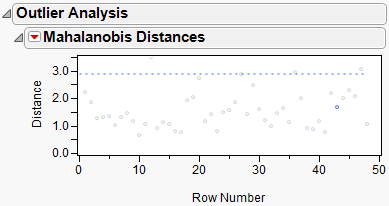
Mahalanobis Distances
plot is commonly used in evaluating classification and cluster analysis techniques. It illustrates the distance of specific
observations
from the
mean
center of the other observations.
Mahalanobis distance
and leverage are often used to detect outliers, especially in the development of linear regression models. A point that has a greater Mahalanobis distance from the rest of the sample
population
of points is said to have higher leverage since it has a greater influence on the slope or coefficients of the
regression
equation. Mahalanobis distance is also used to determine multivariate outliers.
Regression
techniques can be used to determine whether a specific case within a sample
population
is an outlier via the combination of two or more
variable
scores. A point can be a multivariate outlier even if it is not a univariate outlier on any variable.
In the
Mahalanobis Distances
plot shown below, the distance of each row number is plotted. Those outlier points residing above the dotted line correspond to those rows that warrant the most attention due to their significant distance from the mean center of all other observations.