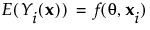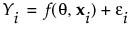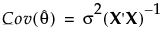Denote the vector of n responses by Y = (Y1, Y2, ..., Yn)‘. A nonlinear model is defined by the following properties:
|
•
|
|
•
|
The expected value of each Yi given a vector of predictor values xi is a nonlinear function of parameters, θ. Denote this function as follows:
|
|
•
|
|
•
|
The vector of errors, ε = (ε1, ε2, ..., εn)‘ has mean 0 and covariance matrix σ2I, where I is the n x n identity matrix.
|
Denote the matrix of first partial derivatives of the function f with respect to the parameters θ by X. Under general conditions, the least squares estimator of θ is asymptotically unbiased, with asymptotic covariance matrix given as follows: