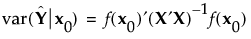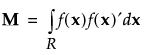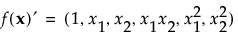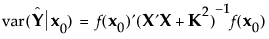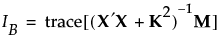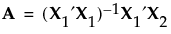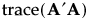Specifically, a D-optimal design maximizes D, where D is defined as follows:
Bayesian D-optimality is a modification of the D-optimality criterion. The Bayesian D-optimality criterion is useful when there are potentially active interactions or non-linear effects. See DuMouchel and Jones (1994) and Jones et al (2008).
|
•
|
X is the model matrix as defined in Simulate Responses
|
|
•
|
K is a diagonal matrix with values as follows:
|
|
–
|
k = 0 for Necessary terms
|
|
–
|
k = 1 for If Possible main effects, powers, and interactions involving a categorical factor with more than two levels
|
|
–
|
k = 4 for all other If Possible terms
|
The prior distribution imposed on the vector of If Possible parameters is multivariate normal, with mean vector 0 and diagonal covariance matrix with diagonal entries 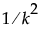 . Therefore, a value
. Therefore, a value 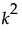 is the reciprocal of the prior variance of the corresponding parameter.
is the reciprocal of the prior variance of the corresponding parameter.
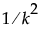 . Therefore, a value
. Therefore, a value 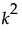 is the reciprocal of the prior variance of the corresponding parameter.
is the reciprocal of the prior variance of the corresponding parameter.The values for k are empirically determined. If Possible main effects, powers, and interactions with more than one degree of freedom have a prior variance of 1. Other If Possible terms have a prior variance of 1/16. In the notation of DuMouchel and Jones, 1994, 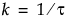 .
.
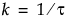 .
.To control the weights for If Possible terms, select Advanced Options > Prior Parameter Variance from the red triangle menu. See Advanced Options > Prior Parameter Variance.
I-optimal designs minimize the integral I of the prediction variance over the entire design space, where I is given as follows:
Here M is the moments matrix:
See Simulate Responses. For further details, see Goos and Jones (2011).
The moments matrix does not depend on the design and can be computed in advance. The row vector f (x)’ consists of a 1 followed by the effects corresponding to the assumed model. For example, for a full quadratic model in two continuous factors, f (x)’ is defined as follows:
|
•
|
X is the model matrix, defined in Simulate Responses
|
|
•
|
K is a diagonal matrix with values as follows:
|
|
–
|
k = 0 for Necessary terms
|
|
–
|
k = 1 for If Possible main effects, powers, and interactions involving a categorical factor with more than two levels
|
|
–
|
k = 4 for all other If Possible terms
|
The prior distribution imposed on the vector of If Possible parameters is multivariate normal, with mean vector 0 and diagonal covariance matrix with diagonal entries 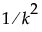 . (See Bayesian D-Optimality for more details about the values k.)
. (See Bayesian D-Optimality for more details about the values k.)
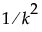 . (See Bayesian D-Optimality for more details about the values k.)
. (See Bayesian D-Optimality for more details about the values k.)Alias optimality seeks to minimize the aliasing between effects that are in the assumed model and effects that are not in the model but are potentially active. Effects that are not in the model but that are of potential interest are called alias effects. For details about alias-optimal designs, see Jones and Nachtsheim (2011).
Specifically, let X1 be the model matrix corresponding to the terms in the assumed model, as defined in Simulate Responses. The design defines the model that corresponds to the alias effects. Denote the matrix of model terms for the alias effects by X2.
The entries in the alias matrix represent the degree of bias associated with the estimates of model terms. See The Alias Matrix in Technical Details for the derivation of the alias matrix.
The sum of squares of the entries in A provides a summary measure of bias. This sum of squares can be represented in terms of a trace as follows:
Designs that reduce the trace criterion generally have lower D-efficiency than the D-optimal design. Consequently, alias optimality seeks to minimize the trace of 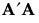 subject to a lower bound on D-efficiency. For the definition of D-efficiency, see Optimality Criteria. The lower bound on D-efficiency is given by the D-efficiency weight, which you can specify under Advanced Options. See Advanced Options > D Efficiency Weight.
subject to a lower bound on D-efficiency. For the definition of D-efficiency, see Optimality Criteria. The lower bound on D-efficiency is given by the D-efficiency weight, which you can specify under Advanced Options. See Advanced Options > D Efficiency Weight.
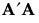 subject to a lower bound on D-efficiency. For the definition of D-efficiency, see Optimality Criteria. The lower bound on D-efficiency is given by the D-efficiency weight, which you can specify under Advanced Options. See Advanced Options > D Efficiency Weight.
subject to a lower bound on D-efficiency. For the definition of D-efficiency, see Optimality Criteria. The lower bound on D-efficiency is given by the D-efficiency weight, which you can specify under Advanced Options. See Advanced Options > D Efficiency Weight.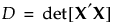
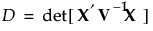
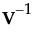 is the block diagonal covariance matrix of the responses (Goos 2002).
is the block diagonal covariance matrix of the responses (Goos 2002).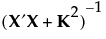 . The Bayesian D-optimal design is obtained by maximizing the determinant of the inverse of the posterior covariance matrix:
. The Bayesian D-optimal design is obtained by maximizing the determinant of the inverse of the posterior covariance matrix: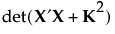
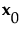 in the design space can be calculated as follows:
in the design space can be calculated as follows: