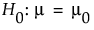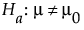where μ is the population mean and μ0 is the null mean to test against or is the difference to detect. It is assumed that the population of interest is normally distributed and the true mean is zero. Note that the power for this setting is the same as for the power when the null hypothesis is H0: μ=0 and the true mean is μ0.
Suppose you are interested in testing the flammability of a new fabric being developed by your company. Previous testing indicates that the standard deviation for burn times of this fabric is 2 seconds. The goal is to detect a difference of 1.5 seconds when alpha is equal to 0.05, the sample size is 20, and the standard deviation is 2 seconds. For this example, μ0 is equal to 1.5. To calculate the power:
|
1.
|
Select DOE > Design Diagnostics > Sample Size and Power.
|
|
2.
|
Click the One Sample Mean button in the Sample Size and Power Window.
|
|
3.
|
Leave Alpha as 0.05.
|
|
4.
|
Leave Extra Parameters as 0.
|
|
5.
|
Enter 2 for Std Dev.
|
|
6.
|
Enter 1.5 as Difference to detect.
|
|
7.
|
Enter 20 for Sample Size.
|
|
8.
|
|
9.
|
Click Continue.
|
The power is calculated as 0.8888478174 and is rounded to 0.89. (See right window in A One-Sample Example.) The conclusion is that your experiment has an 89% chance of detecting a significant difference in the burn time, given that your significance level is 0.05, the difference to detect is 1.5 seconds, and the sample size is 20.
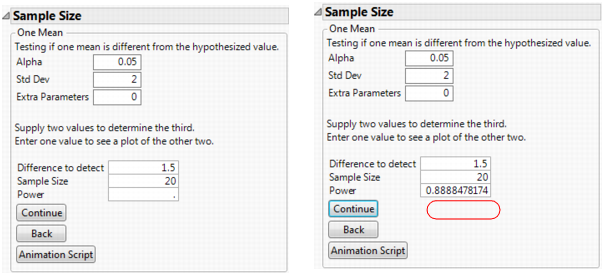
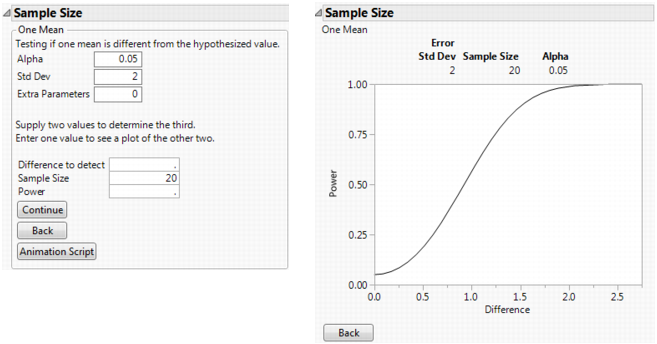
To see a plot of the relationship of Sample Size and Power, leave both Sample Size and Power empty in the window and click Continue.
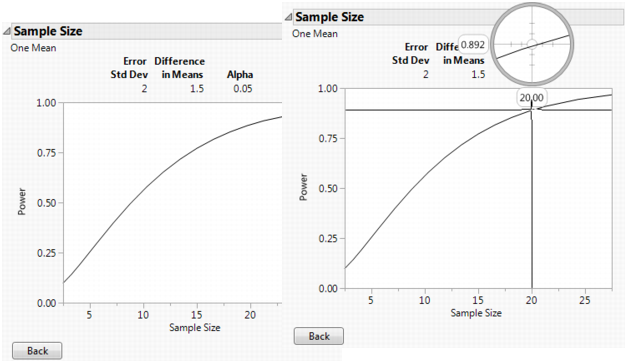
The plots in A One-Sample Example Plot, show a range of sample sizes for which the power varies from about 0.1 to about 0.95. The plot on the right in A One-Sample Example Plot shows using the crosshair tool to illustrate the example in A One-Sample Example.
When only Sample Size is specified (Plot of Power by Difference to Detect for a Given Sample Size) and Difference to Detect and Power are empty, a plot of Power by Difference appears, after clicking Continue.