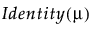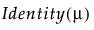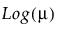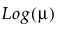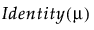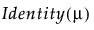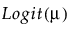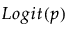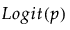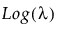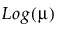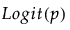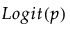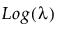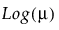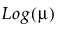When you select Generalized Regression from the Personality menu, the Distribution option appears. Here you can specify a distribution for Y. The abbreviation ZI means zero-inflated. The distributions are separated into three categories based on their response: continuous, discrete, and zero-inflated. The options are described below.
Y has a normal distribution with mean μ and standard deviation σ. The normal distribution is symmetric and with a large enough sample size, can approximate a large variety of other distributions using the Central Limit Theorem. The link function for μ is the identity. That is, the mean of Y is expressed as a linear model.
The scale parameter for the normal distribution is σ. When there is no penalty in the estimation method, the estimate of the scale parameter σ is the root mean square error (RMSE). The RMSE is the square root of the usual unbiased estimator of σ2. The results shown are equivalent to a standard least squares fit unless censored observations are involved.
Y has a Cauchy distribution with location parameter μ and scale parameter σ. The Cauchy distribution has an undefined mean and standard deviation. The median and mode are both μ. Most data do not inherently follow a Cauchy distribution. However, it is useful for conducting a robust regression on data that contain a large proportion of outliers (up to 50%). The link function for μ is the identity. See Statistical Details for Distributions.
Y has an exponential distribution with mean parameter μ. The exponential distribution is right-skewed and is often used to model lifetimes or the time between successive events. The link function for μ is the logarithm. See Statistical Details for Distributions.
Y has a gamma distribution with mean parameter μ and dispersion parameter σ. The gamma is a flexible distribution and contains a family of other widely used distributions. For example, the exponential distribution is a special case of the gamma distribution where σ = μ. The chi squared distribution can also be derived from the gamma distribution. The link function for μ is the logarithm. See Statistical Details for Distributions.
Y has a Weibull distribution with mean parameter μ and scale parameter σ. The Weibull distribution is flexible and is often used to model lifetimes or the time until an event. The link function for μ is the identity. See Statistical Details for Distributions.
Y has a Lognormal distribution with mean parameter μ and scale parameter σ. The Lognormal distribution is right-skewed and is often used to model lifetimes or the time until an event. The link function for μ is the identity. See Statistical Details for Distributions.
Y has a beta distribution with mean parameter μ and dispersion parameter σ. The response for the beta is between 0 and 1 (not inclusive) and is often used to model proportions or rates. The link function for μ is the logit. See Statistical Details for Distributions.
Quantile Regression is fit by minimizing an objective function using an iterative approach. For more information about quantile regression, see Koenker and Hallock (2001) and Portnoy and Koenker (1997).
The Cox proportional hazards model is a regression model for time-to-event data with predictors. It is based on a multiplicative relationship between the predictors and the hazard function. It can be used to examine the effect of predictors on survival times. The model involves an arbitrary baseline hazard function that is scaled by the predictors to give a general hazard function. The proportional hazards model produces parameter estimates and standard errors for each predictor. The Cox proportional hazards model was first proposed by D. R. Cox (1972). For more information about proportional hazards models, see Kalbfleisch and Prentice (2002).
Note: When there are ties in the response, the Efron likelihood is used. See Efron (1977). This is a different method for handling ties than is used in the Proportional Hazard personality of the Fit Model platform or in the Fit Proportional Hazards platform.
Y has a binomial distribution with parameters p and n. The response, Y, indicates the total number of successes in n independent trials with a fixed probability, p, for all trials. This distribution allows for the use of a sample size column. If no column is listed, it is assumed that the sample size is one. The link function for p is the logit. When you select a binary response variable that has a Nominal modeling type, Binomial is the only available response distribution. See Statistical Details for Distributions.
Y has a beta binomial distribution with the probability of success, p, the number of trails, n, and overdispersion parameter, δ. This distribution is an overdispersed version of the binomial distribution.
Run demoBetaBinomial.jsl in the JMP Samples/Scripts folder to compare a beta binomial distribution with dispersion parameter δ to a binomial distribution with parameters p and n = 20.
The beta binomial distribution requires a sample size greater than one for each observation. Thus, the user must specify a sample size column. To insert a sample size column, specify two continuous columns as Y in this order: the count of the number of successes, and the count of the number of trials. The link function for p is the logit. See Statistical Details for Distributions.
Y has a multinomial distribution with three or more discrete levels. The response variable must have a nominal or ordinal modeling type. The model fits separate intercepts and effects parameters for each level of the response variable. If the response variable has k levels, the model contains k - 1 intercepts and effects parameters. The link function for the Multinomial distribution is the multinomial logit. See Nominal Responses in Statistical Details.
Y has a multinomial distribution with ordinal levels. The response variable must have an ordinal modeling type. The model fits an intercept for each level of the response variable. The effects parameters are common across all levels of the response variable. The link function for the Ordinal Logistic distribution is the ordered logit. See Ordinal Responses in Statistical Details.
Y has a Poisson distribution with mean λ. The Poisson distribution typically models the number of events in a given interval and is often expressed as count data. The link function for λ is the logarithm. Poisson regression is permitted even if Y assumes non-integer values. See Statistical Details for Distributions.
Y has a negative binomial distribution with mean μ and dispersion parameter σ. The negative binomial distribution typically models the number of successes before a specified number of failures. The negative binomial distribution is also equivalent to the Gamma Poisson distribution under certain conditions. For more details about the connection between negative binomial and Gamma Poisson, see Distributions in the Basic Analysis book.
Run demoGammaPoisson.jsl in the JMP Samples/Scripts folder to compare a Gamma Poisson distribution with mean λ and dispersion parameter σ to a Poisson distribution with mean λ.
The link function for μ is the logarithm. Negative binomial regression is permitted even if Y assumes non-integer values. See Statistical Details for Distributions.
Y has a zero-inflated binomial distribution with parameters p, n, and zero-inflation parameter π. The response, Y, indicates the total number of successes in n independent trials with a fixed probability, p, for all trials. This distribution allows for the use of a sample size column. If no column is listed, it is assumed that the sample size is one. The link function for p is the logit. See Statistical Details for Distributions.
Y has a beta binomial distribution with the probability of success, p, the number of trails, n, overdispersion parameter, δ, and zero-inflation parameter π. This distribution is an overdispersed version of the ZI binomial distribution. The ZI beta binomial distribution requires a sample size greater than one for each observation. Thus, the user must specify a sample size column. To insert a sample size column, specify two continuous columns as Y in this order: the count of the number of successes, and the count of the number of trials. The link function for p is the logit. See Statistical Details for Distributions.
Y has a zero-inflated Poisson distribution with mean parameter λ and zero-inflation parameter π. The parameter λ is the conditional mean based on the observations coming from the Poisson distribution and not the inflating zeros. The link function for λ is the logarithm. ZI Poisson regression is permitted even if Y assumes no observed zeros or non-integer values. See Statistical Details for Distributions.
Y has a zero-inflated negative binomial with location parameter μ, dispersion parameter σ, and zero-inflation parameter π. The parameter μ is the conditional mean based on the observations coming from the negative binomial distribution and not the inflating zeros. The link function for μ is the logarithm. ZI negative binomial regression is permitted even if Y assumes no observed zeros or non-integer values. See Statistical Details for Distributions.
Y has a zero-inflated gamma distribution with mean parameter μ and zero-inflation parameter π. Many times, we might believe that our nonzero responses are gamma distributed. This is true for insurance claims: claim values are approximately gamma distributed but there are also zeros in the data for policies that do not have any claims. The zero-inflated gamma could handle such data directly without having to split the data into zero and nonzero responses. The parameter μ is the conditional mean based on observations coming from the gamma distribution and not the inflating zeros. The link function for μ is the logarithm. See Statistical Details for Distributions.
Table 5.1 gives the Data Types, Modeling Types, and other requirements for Y variables assigned the various distributions.
For more information about how these distributions are parameterized, see Statistical Details for Distributions. Table 5.2 summarizes the details.
|
μ, σ
|
||
|
μ, σ
|
||
|
μ, σ
|
||
|
μ, σ
|
||
|
μ, σ
|
||
|
n, p
|
||
|
μ, σ
|
||
|
λ, π (zero-inflation)
|
||
|
μ, σ, π (zero-inflation)
|
||
|
μ, σ, π (zero-inflation)
|
After selecting an appropriate Distribution, click Run. The Generalized Regression report window appears.