Fitting Linear Models • Mixed Models • Additional Examples
Previous
 • 
Next
Additional Examples
Repeated Measures Example
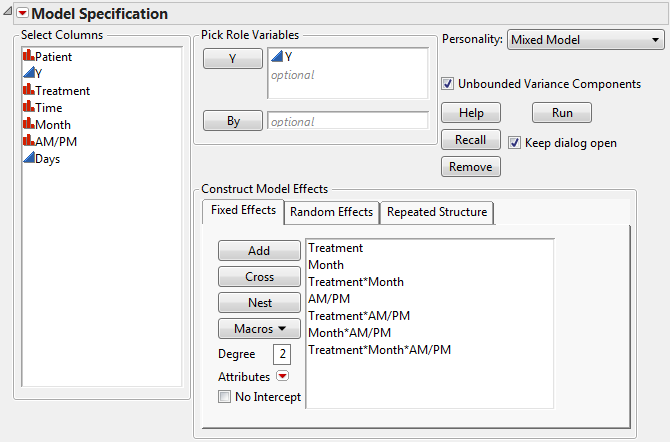
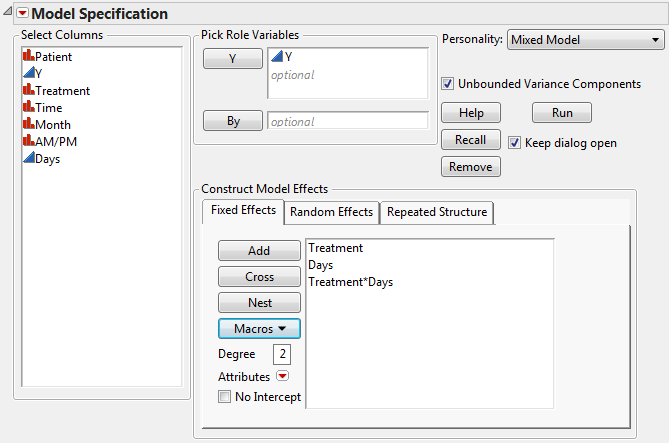
Consider the Cholesterol Stacked.jmp sample data table. A study was performed to test two new cholesterol drugs against a control drug. Five patients with high cholesterol were randomly assigned to each of four treatments (the two experimental drugs, the control, and a placebo). Each patient’s total cholesterol was measured at six times during the study: the first day in April, May, and June in the morning and afternoon. You are interested in whether either of the new drugs is effective at lowering cholesterol and in whether time and treatment interact.
Two methods have historically been used to analyze such a design: multivariate analysis of variance (MANOVA) or a split-plot in time univariate analysis of variance (ANOVA) with either the Huynh-Feldt (1976) or Greenhouse-Geisser (1959) correction. Both of these options are available using the MANOVA personality in Fit Model. These two options are the two extremes for modeling the covariance structure. The MANOVA analysis assumes an unstructured covariance structure where all variances and covariances are estimated individually. The independent split-plot in time analysis assumes that all errors are independent. In the Gaussian data case, this is equivalent to assuming a compound symmetry covariance structure.
These two models can result in vastly different conclusions about the treatment effects. When you assume a complex covariance structure, information in the data is used to estimate the covariance parameters. Therefore, it is important to find a model appropriate for the data. If you fit too many covariance parameters, you run the risk of overfitting your model.
•
When the model is overfit, the power to detect differences is smaller than if you were to assume a less complex covariance structure.
•
When the model is underfit, Type I error control is lost. In some cases, this leads to inflated rejection rates. In other cases, decreased rejection rates occur due to inflated variance.
When you model repeated measures data, be careful to find the appropriate covariance structure to balance these issues.
The Mixed Model personality fits a variety of covariance structures. For repeated measures in time, the first-order autoregressive (AR(1)) covariance structure often provides an appropriate correlation structure. This structure allows for correlated observations but without overfitting the model.
Suppose that your model has J observation times. Then the number of covariance parameters in the covariance matrices for the three structures available are as follows:
•
Unstructured, J(J+1)/2
•
AR(1), 2
•
Independent Split Plot, 2
See Repeated Measures for more information.
Open Cholesterol.jmp to see a format that is typically used for recording repeated measures data. For Mixed Model analysis of this data, each cholesterol measurement needs to be in its own row, as in Cholesterol Stacked.jmp. To construct Cholesterol Stacked.jmp, the data in Cholesterol.jmp was stacked using Tables > Stack.
The Days column in the stacked table was constructed using a formula. The Days column gives the number days into the study when the cholesterol measurement was taken. Its modeling type is continuous. This is necessary because the AR(1) covariance structure requires the repeated effect be continuous.
The first step is to choose the appropriate covariance structure for these data. You fit the three covariance structures:
•
Unstructured: This model fits all covariance parameters.
•
Residual: This model is equivalent to the usual variance components structure. In this case, the model fits two variances.
•
AR(1): This model fits two covariance parameters, one of which determines how the covariance changes with time.
You evaluate the model fits using AICc. The BIC criterion can also be used. In this case, the same model is chosen by both criteria.
Tip: This section walks you through many aspects of fitting repeated measures (from fitting the model to deciding on the best covariance structure). Leave the Fit Model launch window open as you work through each example.
Covariance Structure: Unstructured Example
Begin by fitting a model using an Unstructured covariance structure.
1.
Select Help > Sample Data Library and open Cholesterol Stacked.jmp.
2.
Select Analyze > Fit Model.
3.
Select Keep dialog open so that you can return to the launch window in the next example.
4.
Select Y and click Y.
5.
Select Mixed Model from the Personality list.
6.
Select Treatment, Month, and AM/PM, and then select Macros > Full Factorial.
Fit Model Launch Window Showing Completed Fixed Effects Tab
7.
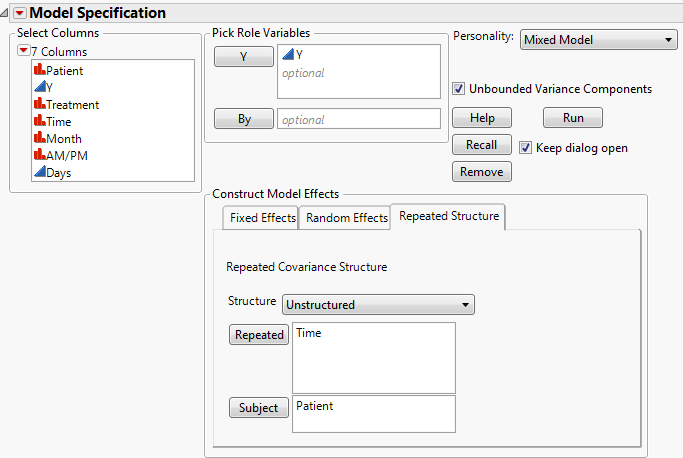
Select the Repeated Structure tab.
8.
Select Unstructured from the Structure list.
9.
Select Time and click Repeated. The Repeated column defines the repeated measures within a subject.
10.
Select Patient and click Subject.
Note: The Unstructured covariance model does not allow duplicate values on the repeated structure variables. Suppose that, in this example, the subject was nested within treatment, and that the patients had been numbered using the values 1, 2, 3, 4, and 5 within each treatment. A warning would be given when you run this analysis. You would need to renumber the patients to have different identifiers for each value of the Repeated variable. Or you would need to create a column in the data table that represents nesting within treatment and enter this effect as Subject.
Fit Model Launch Window Showing Completed Repeated Structure Tab
11.
Click Run.
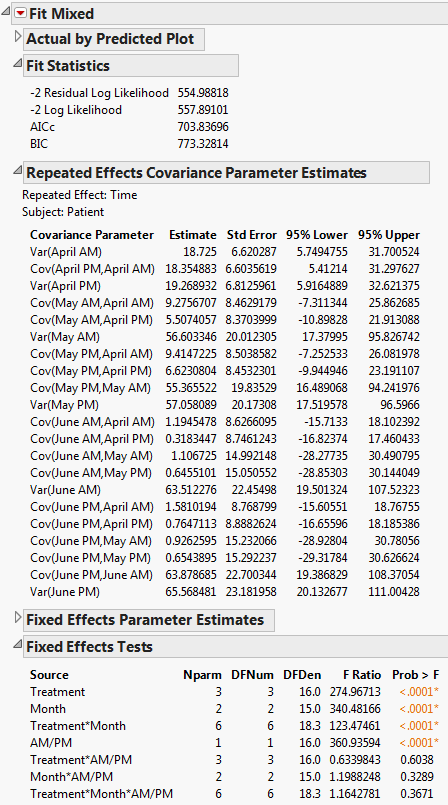
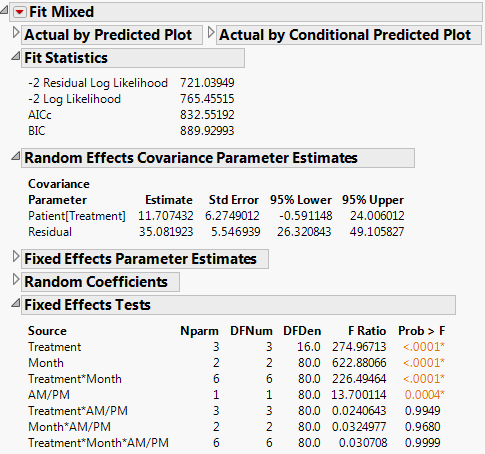
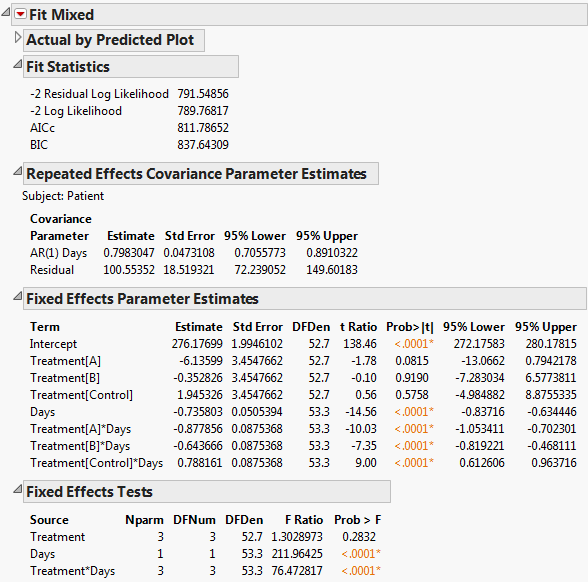
The Fit Mixed report is shown in Fit Mixed Report - Unstructured Covariance Structure. Because you want to compare your three models using AICc or BIC, you are interested in the Fit Statistics report. The AICc for the unstructured model is 703.84.
The Repeated Effects Covariance Parameter Estimates report shows estimates of all 21 covariance parameters. As you would expect, observations taken closer in time have higher covariance than those farther apart. Also, variance increases with time.
Fit Mixed Report - Unstructured Covariance Structure
Covariance Structure: Residual Example
The Residual covariance structure is appropriate when you fit a split-plot model.
1.
Complete step 1 through step 7 in Covariance Structure: Unstructured Example.
2.
On the Repeated Structure tab, select Residual from the Structure list.
3.
If you are continuing from the previous example, remove Time and Patient. Otherwise, a warning appears: “Repeated columns and subject columns are ignored when the Residual covariance structure is selected.” You are given the option to click OK to continue the analysis.
4.
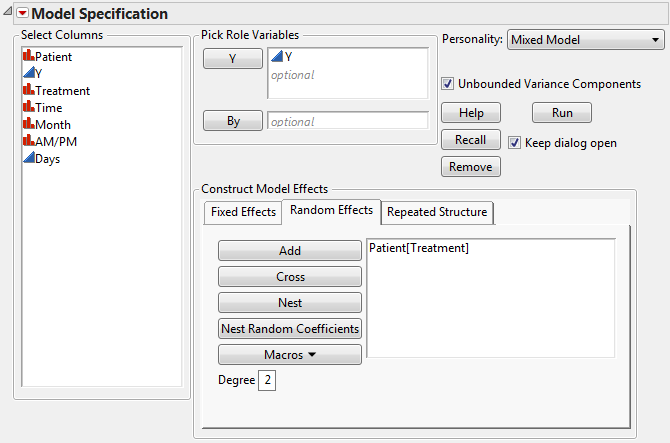
Select the Random Effects tab.
5.
Select Patient and click Add.
6.
Select Patient in the Random Effects area, select the Treatment column, and then click Nest.
Fit Model Launch Window Showing Completed Random Effects Tab
7.
Click Run.
The Fit Mixed report is shown in Fit Mixed Report - Residual Error Covariance Structure. The Fit Statistics report shows that the AICc for the Residual model is 832.55, as compared to 703.84 for the Unstructured model.
The estimates of the two covariance parameters are shown in the Random Effects Covariance Parameter Estimates report. These are estimates of the variance of Patient within Treatment, and of the Residual variance.
Fit Mixed Report - Residual Error Covariance Structure
Covariance Structure: AR(1) Example
Finally, fit the AR(1) structure.
1.
Complete step 1 through step 6 in Covariance Structure: Unstructured Example.
2.
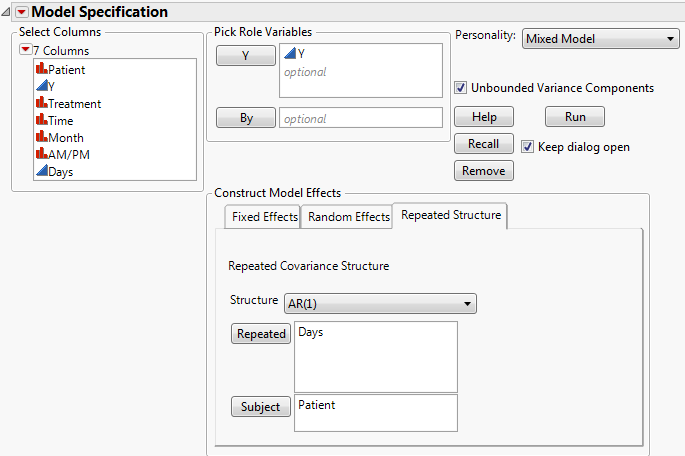
If you are continuing from the previous example, select Patient[Treatment] on the Random Effects tab and then click Remove.
If you include both random effects and repeated effects, there is often insufficient data to estimate both effects.
3.
Select the Repeated Structure tab.
4.
Select AR(1) from the Structure list.
5.
Select Days and click Repeated.
6.
Select Patient and click Subject.
Fit Model Launch Window Showing Completed Repeated Effects Tab
7.
Click Run.
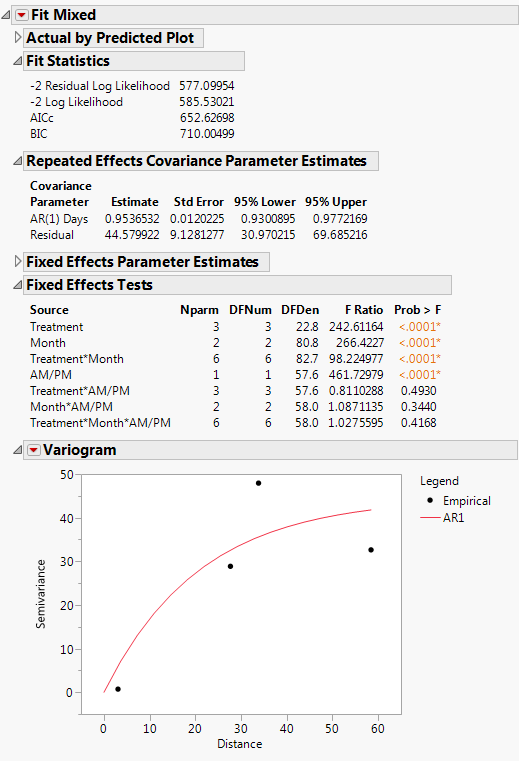
The Fit Mixed report is shown in Fit Mixed Report - AR(1) Covariance Structure. The Fit Statistics report shows that the AICc for the AR(1) model is 652.63, compared with 832.55 for the Residual model and 703.84 for the Unstructured model. Based on the AICc criterion, the AR(1) model is the best of the three models.
The AR(1) structure requires the estimation of two covariance parameters. These estimates are shown in the Repeated Effects Covariance Parameter Estimates report. The AR(1) Days parameter estimate is an estimate of ρ, the correlation parameter in the AR(1) structure.
The Variogram plot shows the empirical semivariances and the curve for the AR(1) model. Since there are only five non-zero values for Days, only four distance classes are possible and only four points are shown. The AR(1) structure seems appropriate. To explore other structures, select options from the red triangle menu next to Variogram.
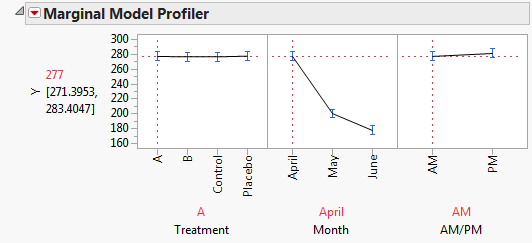
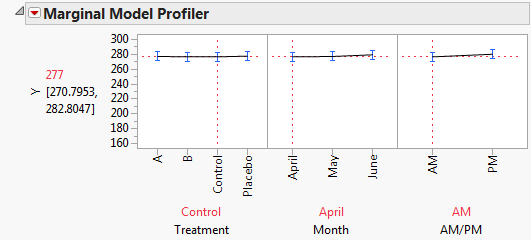
Fit Mixed Report - AR(1) Covariance Structure
Because the AR(1) model gives the best fit, you adopt it as your model and proceed with your analysis. The Fixed Effects Tests report indicates that there is a significant interaction between Treatment and Month as well as a main effect of AM/PM.
To explore these significant effects, select Marginal Model Inference > Profiler from the Fit Mixed report’s red triangle menu. The Marginal Model Profiler report (Marginal Profiler Plot for Treatment A) shows that, for Treatments A and B, cholesterol levels (Y) decrease steadily over the three months. However, when you set Treatment to Control or Placebo, you see virtually no change over the three months (Marginal Profiler Plot for Control).
Note that Treatment A seems to result in lower cholesterol readings in May than Treatment B does. If this effect is significant, it might indicate that Treatment A acts more quickly than B. The next section, Compare All Treatments in June, shows you how to evaluate the treatments.
The profiler also shows the main effect of AM/PM. To obtain the profiler, select Marginal Model Inference > Profiler. By setting Treatment and Month to all 12 combinations of their levels, you see that the predicted cholesterol level is consistently higher in the afternoon than in the morning.
Marginal Profiler Plot for Treatment A
Marginal Profiler Plot for Control
Compare All Treatments in June
The study is conducted over the months of April, May, and June. You are interested in which treatments differ on the PM measurement in June.
1.
Select Multiple Comparisons from the Fit Mixed red triangle menu.
2.
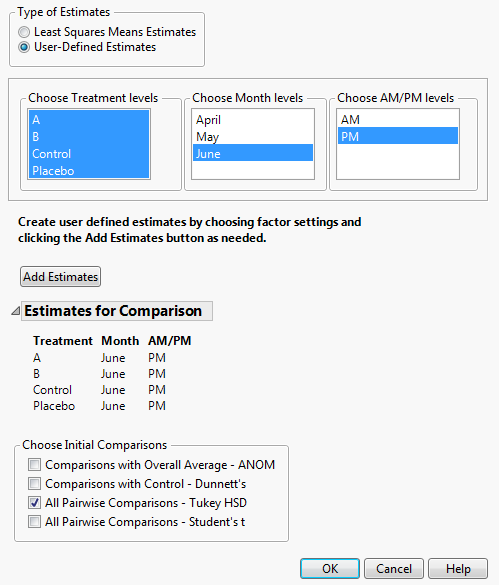
Under Types of Estimates, select User-Defined Estimates.
3.
From the Choose Treatment levels panel, select all four treatment types.
4.
From the Choose Month levels panel, select June.
5.
From the Choose AM/PM levels panel, select PM.
6.
Click Add Estimates.
7.
From the Choose Initial Comparisons list, select All Pairwise Comparisons - Tukey HSD.
The Multiple Comparisons window should appear as shown in Completed Multiple Comparisons Window.
Completed Multiple Comparisons Window
8.
Click OK.
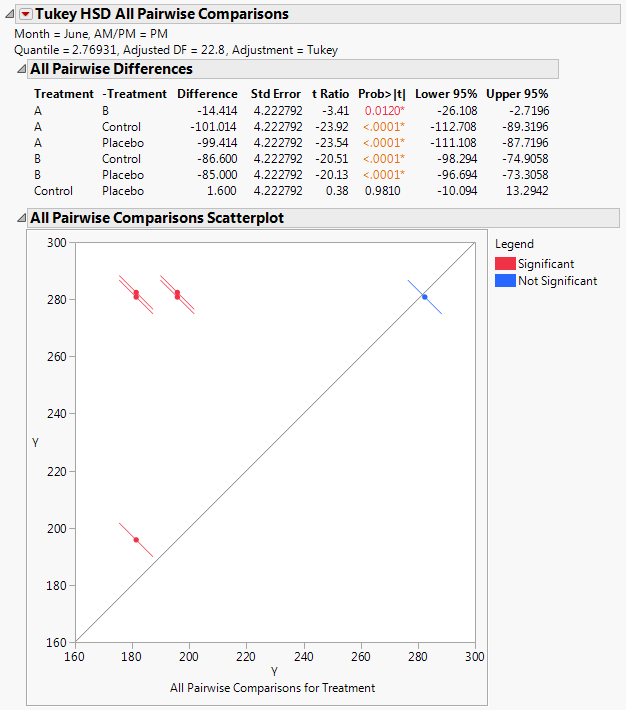
The Tukey HSD All Pairwise Comparisons report shows an All Pairwise Differences report and an All Pairwise Comparisons Scatterplot (Tukey HSD All Pairwise Comparisons Report for All Treatments for June PM). All treatments other than the Control and Placebo differ significantly on the June PM measurements.
Consider the difference between treatments A and B. The difference in means is -14.414 and the confidence interval ranges from -26.108 to -2.7196. You conclude that the reduction in cholesterol measurements due to treatment A exceeds the reduction by treatment B by somewhere between 2.7 and 26.1 points. Both treatments A and B are highly effective compared to the Control and Placebo.
Tukey HSD All Pairwise Comparisons Report for All Treatments for June PM
Conduct an Equivalence Test
Suppose that the scientist with whom you are working considers a change of no more than three points to be equivalent to zero change from a practical perspective. Conduct an equivalence test to see whether the effect of AM/PM is of practical interest.
1.
Select Multiple Comparisons from the Fit Mixed red triangle menu.
2.
Select AM/PM from the Choose an Effect list.
3.
Select All Pairwise Comparisons - Tukey HSD from the Choose Initial Comparisons list.
4.
Click OK.
The report shows that the estimated difference between the afternoon and morning observations is 4.00261. Though this is statistically significant, is it sufficiently larger than 3.0 to be considered not equivalent to 3.0?
5.
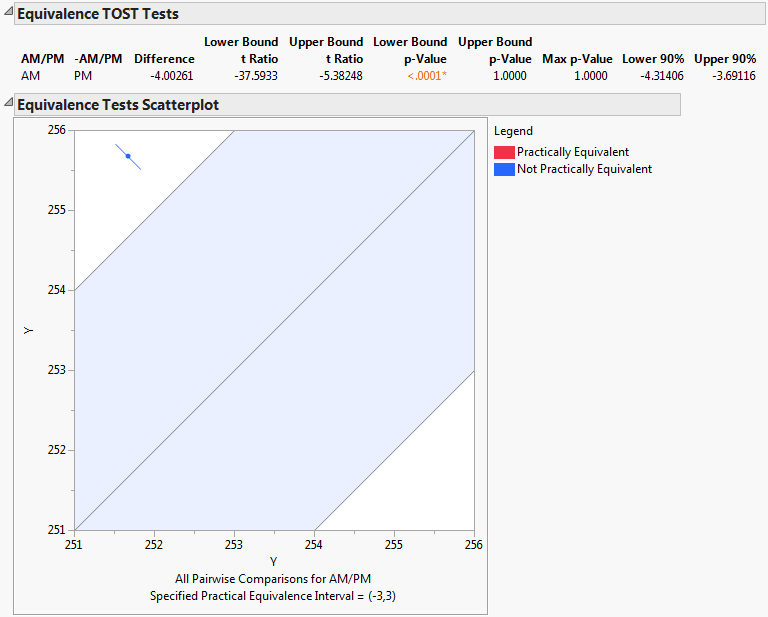
Select Equivalence Tests from the Tukey HSD All Pairwise Comparisons red triangle menu.
6.
Type 3 in the box for Difference considered practically zero.
7.
Click OK.
The Equivalence TOST Tests report and Equivalence Test Scatterplot show that the -4.00261 point difference is not equivalent to zero, and so is of practical interest.
Equivalent TOST Test and Equivalence Test Scatterplot for AM/PM Effect
Note: In order to conclude that the difference is of practical significance, you need to test and reject the null hypothesis that the absolute difference is less than three.
Regression Model for AR(1) Model Example
Using the Month and AM/PM categorical effects, you have compared three covariance structures for the cholesterol data. (Note that a categorical effect was required for the Unstructured fit.) You have decided to use an AR(1) covariance structure.
Suppose now that you want to model the effect of treatment in terms of the continuous effect Days instead of the categorical effects. You can then predict cholesterol levels at arbitrary time during treatment.
1.
After following steps in Covariance Structure: AR(1) Example, return to the Fit Model launch window.
2.
On the Fixed Effects tab, select the existing fixed effects and click Remove.
3.
Select Treatment and Days then select Macros > Full Factorial.
Fit Model Launch Window Showing Fixed Effects Tab
4.
Click Run.
The Fit Mixed report is shown in Fit Mixed Report - AR(1) Covariance Structure with Continuous Fixed Effect. You see that the interaction of Treatment and Days is highly significant indicating different regressions for the drugs.
Note: To predict outcomes for the drugs at different days, use the profiler. See the Profilers book for more information.
Fit Mixed Report - AR(1) Covariance Structure with Continuous Fixed Effect
Split Plot Example
The Mixed Model personality offers a straightforward approach to specifying and analyzing split-plot experiments. Mixed Model provides tabs for specifying effects. The resulting analysis is targeted to random effects. Note, however, that split-plot experiments can also be analyzed using the Standard Least Squares personality.
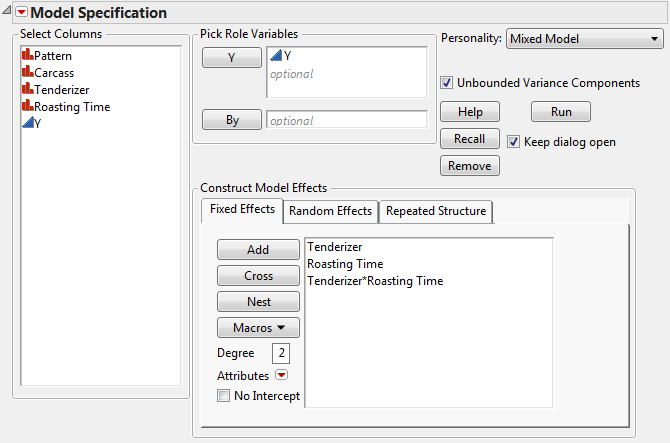
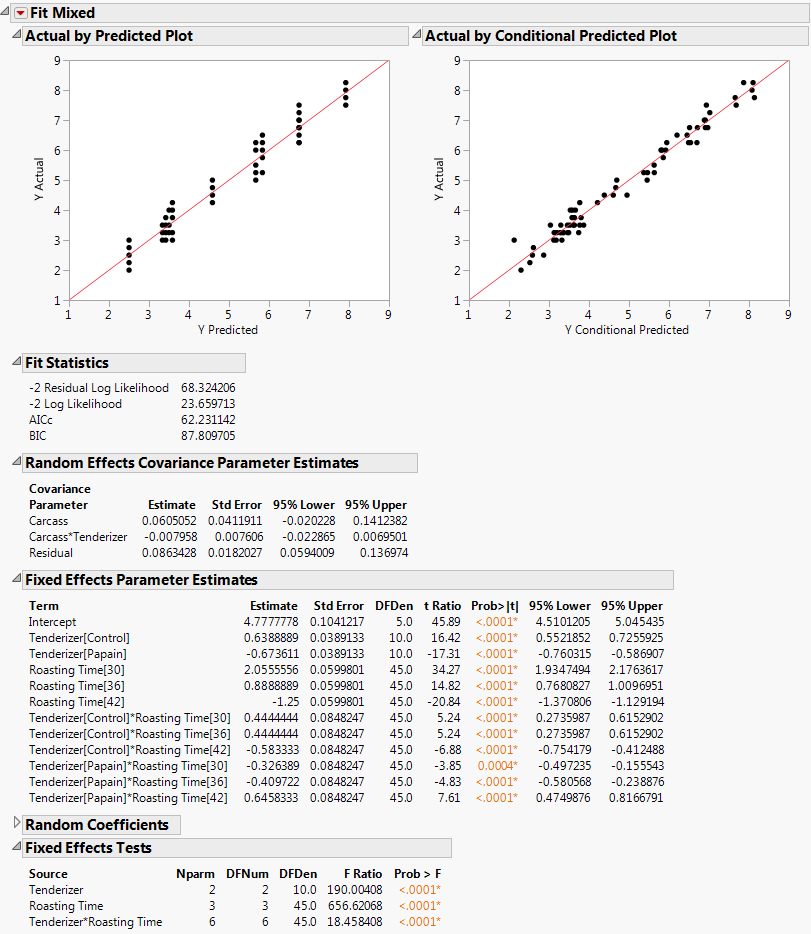
The data in the Split Plot.jmp sample data table come from a study of the effects of tenderizer and length of cooking time on meat. Six beef carcasses were randomly selected from carcasses at a meat packaging plant. From the right rib-eye muscle of each carcass, three rolled roasts were prepared under uniform conditions. Each of these three roasts was assigned a tenderizing treatment at random. After treatment, a coring device was used to mark four cores of meat near the center of each.
The three roasts from the same carcass were placed together in a preheated oven and allowed to cook. After 30 minutes, one of the cores was taken at random from each roast. Cores were removed in this fashion again after 36 minutes, 42 minutes, and 48 minutes. As each set cooled to serving temperature, the cores were measured for tenderness using the Warner-Bratzler device. Larger measurements indicate tougher meat.
Your interest centers on the effects of tenderizer, roasting time, and especially whether there is an interaction between tenderizer and roasting time. This design addresses that goal.
1.
Select Help > Sample Data Library and open Split Plot.jmp.
2.
Select Analyze > Fit Model.
3.
Select Y and click Y.
4.
Select Mixed Model from the Personality list.
5.
Select Tenderizer and Roasting Time, and then select Macros > Full Factorial.
Fit Model Launch Window Showing Completed Fixed Effects Tab
6.
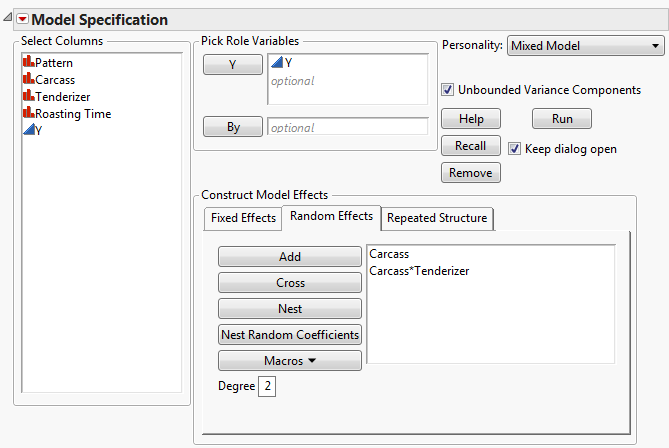
Select the Random Effects tab.
7.
Select Carcass and click Add to create the random carcass effect.
8.
Select Carcass and Tenderizer and click Cross.
The Carcass*Tenderizer interaction is the error term for the whole plot factor, Tenderizer. This is equivalent to the Carcass*Tenderizer&Random term in Standard Least Squares.
Fit Model Launch Window Showing Completed Random Effects Tab
9.
Click Run.
The Fit Mixed report is shown in Fit Mixed Report.
The Actual by Predicted Plot and the Actual by Conditional Predicted Plot show no issues with model fit, so you can proceed to interpret the results. The Fixed Effects Tests report indicates that there is a significant interaction between tenderizer and roasting time.
Fit Mixed Report
Explore the Interaction between Tenderizer and Roasting Time
1.
Select Marginal Model Inference > Profiler from the Fit Mixed report’s red triangle menu.
Marginal Model Profiler with Roasting Time Set to 30 Minutes
2.
Move the red dashed vertical line in the Roasting Time panel to 36, 42, and 48.
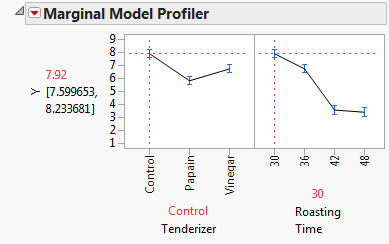
In Marginal Model Profiler with Roasting Time Set to 30 Minutes, notice that both the papain and vinegar tenderizers result in significantly lower tenderness scores than the control when roasting time is either 30 or 36 minutes. However, at 42 minutes, there are no significant differences. At 48 minutes, papain gives a value lower than the control, but vinegar does not. Papain gives lower tenderness scores than does vinegar at all times except 42 minutes.
3.
Select Multiple Comparisons from the Fit Mixed red triangle menu.
4.
Select Tenderizer*Roasting Time.
5.
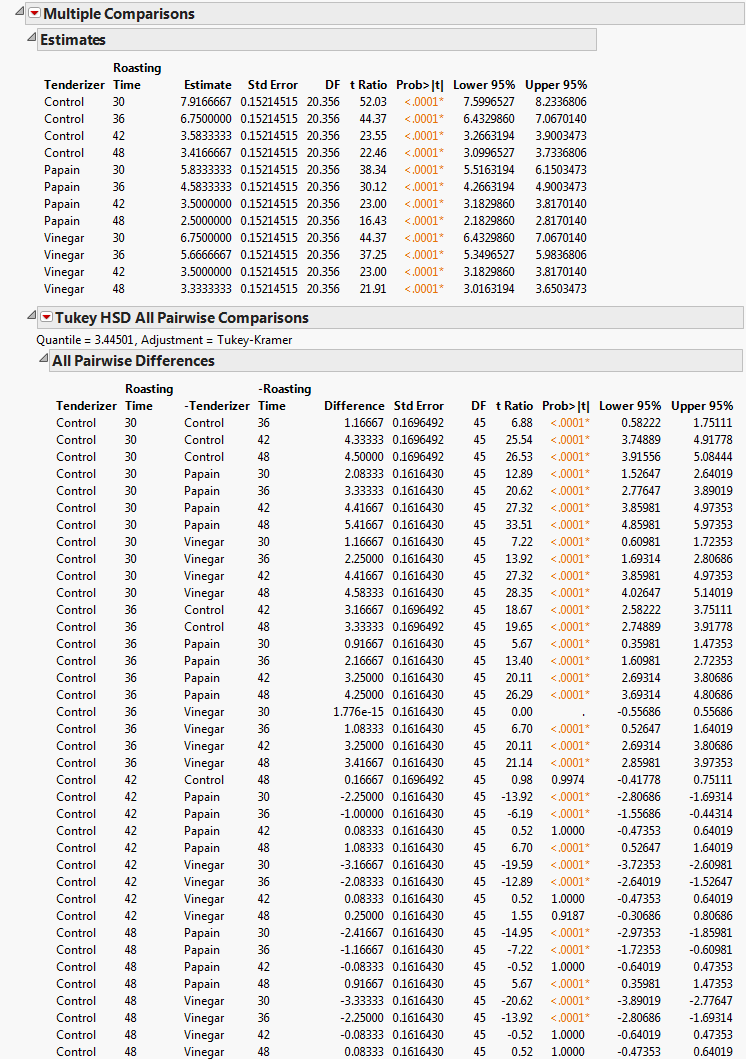
Select All Pairwise Comparisons - Tukey HSD and then click OK.
Multiple Comparisons, Partial View shows a partial list of pairwise comparisons. Most of the differences between papain and vinegar that you observed in the profiler are statistically significant. Therefore, it appears that papain is the better tenderizer.
Multiple Comparisons, Partial View
Spatial Example: Uniformity Trial
Consider the Uniformity Trial.jmp sample data table. An agronomic uniformity trial was conducted on an 8x8 grid of plots. In a uniformity trial, a test crop is grown on a field with no experimental treatments applied. The response variable, often yield, is measured. The idea is to characterize variability in the field as background for planning a designed experiment to be conducted on that field. (See SAS for Mixed Models, 2nd Edition, 2006, pp. 447.)
Your objective is to use the information from these data to design a yield trial with 16 treatments. Specifically, you want to decide whether to conduct future experiments on the field as follows:
•
a complete block design with 4 blocks (denoted Quarter in the data)
•
an incomplete block design with 16 blocks (denoted Subquarter in the data)
•
a completely randomized design with spatially correlated errors
With this objective, spatial data can be treated as repeated measures with two or more dimensions as repeated effects. So, you can compare and choose an appropriate model using the values in the Fit Statistics report. You start by determining if there is significant spatial variability, then you determine whether there is a nugget effect.
Once you have established whether there is a nugget effect, you determine the best fitting spatial covariance structure. Finally, you fit the blocking models and compare these to the best spatial structure. In this example, both AICc and BIC are used to select a best model. Spatial and Temporal Variability provides more information about nugget effects and other spatial terminology.
Tip: This section walks you through many aspects of fitting spatial data (from fitting the model to deciding on the best covariance structure). Leave the Fit Model launch window open as you work through each example.
Fit a Spatial Structure Model
To determine whether there is significant spatial variability, you can fit a model that accounts for spatial variability. Then you can compare the likelihood for this spatial model to the likelihood for a model that does not account for spatial variability. You can do this because the independent errors model is nested within the spatial model family: The independent errors model is a spatial model with spatial correlation, ρ, equal to 0. This means that you can perform a formal likelihood ratio test of the two models.
First, fit the model that accounts for spatial structure.
1.
Select Help > Sample Data Library and open Uniformity Trial.jmp.
2.
Select Analyze > Fit Model.
3.
Select Keep dialog open so that you can return to the launch window in the next example.
4.
Select Yield and click Y.
5.
Select Mixed Model from the Personality list.
6.
Select the Repeated Structure tab.
7.
Choose Spatial from the list next to Structure.
8.
Choose Spherical from the list next to Type.
9.
Select Row and Column and click Repeated.
Completed Fit Model Launch Window Showing Repeated Structure Tab
10.
Click Run.
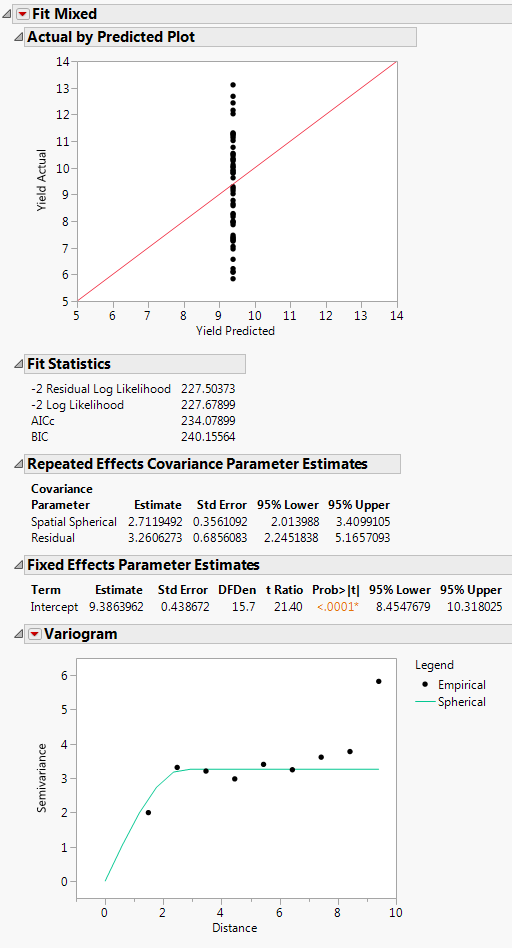
The Fit Mixed report is shown in Fit Mixed Report - Spatial Spherical. The Actual by Predicted Plot shows that the predicted yield is a single value. This is because only spatial covariance was fit. The Fit Statistics report shows that -2 Log Likelihood is 227.68, and the AICc is 234.08.
Because an isotropic spatial structure was fit, a Variogram plot is shown. Because the trials are laid out in an 8 by 8 grid, there will be more pairs of points at small distances than at very large distances. See Graph Builder Plot of Proposed Complete and Incomplete Block Designs for the layout. The Variogram shows that a spherical spatial structure is an excellent fit for distances up to about 8.4. The distance class for the final distance consists of only the two diagonal pairs of points.
The Repeated Effects Covariance Parameter Estimates report gives estimates of the range (Spatial Spherical = 2.71) and the sill (Residual = 3.26). See Variogram.
Fit Mixed Report - Spatial Spherical
Fit the Independent Errors Model
Next, fit the independent errors model.
1.
Return to the Fit Model Launch Window.
2.
Select Repeated Structure tab.
3.
Select Residual from the Structure list.
4.
Remove Row and Column from the Repeated effects list. Otherwise, a warning appears: “Repeated columns and subject columns are ignored when the Residual covariance structure is selected.”
5.
Click Run.
The fit statistics for the independent errors model are: -2 Log Likelihood = 254.22, and AICc = 258.41. Each of these exceeds the corresponding value for the spatial correlation model, where -2 Log Likelihood is 227.68 and the AICc is 234.08. Because smaller values of these statistics indicate a better fit, the spatial model might provide a better fit.
Conduct a Likelihood Ratio Test (Optional)
A formal likelihood ratio test shows whether the spatial correlation model explains significant variation. One model must be nested in another model to create valid likelihood ratio tests.
Typically, spatial models are compared using AICc or BIC rather than through formal likelihood ratio testing. Evaluating the AICc or BIC is faster, and many spatial models are not nested.
You can conduct a likelihood ratio test in this example, because the independent errors model is nested within the spatial model family. The independent errors model is a spatial model with spatial correlation, ρ, equal to 0. This means that you can perform a formal likelihood ratio test of the two models.
In this example, the likelihood ratio test statistic is 254.22-227.68=26.54. Comparing this to a Chi-square distribution on one degree of freedom, the null hypothesis of no spatial correlation is rejected with a p-value < 0.0001. You can conclude that these data contain significant spatial variability.
Select the Type of Spatial Covariance
Next, you determine which spatial covariance structure best fits the data:
•
with or without a nugget effect (variation over relatively small distances)
•
isotropic (spatial correlation is equal in all directions) or anisotropic (spatial correlation differs in the two directions)
•
type of structure, spherical, Gaussian, exponential, or power.
1.
Return to the Fit Model launch window.
2.
Select the Repeated Structure tab.
3.
Select Row and Column and click Repeated.
4.
Select Spatial with Nugget from the Structure list.
5.
Select Spherical from the Type list.
6.
Click Run.
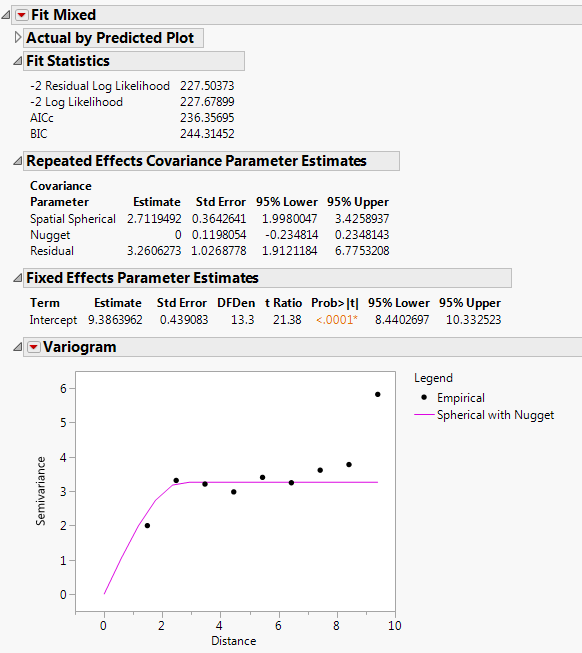
The Fit Mixed report is shown in Fit Mixed Report - Spatial Spherical with Nugget. Notice that the log likelihoods are essentially equal to those of the spherical with no nugget model, and the AICc is slightly higher (236.36 compared to 234.08). The Repeated Effects Covariance Parameter Estimates report shows that the Nugget covariance parameter has an estimate of zero. There does not appear to be any evidence for a nugget effect.
Fit Mixed Report - Spatial Spherical with Nugget
7.
From the red triangle menu next to Variogram, select Spatial > Spherical.
Fit Mixed Report - Variogram
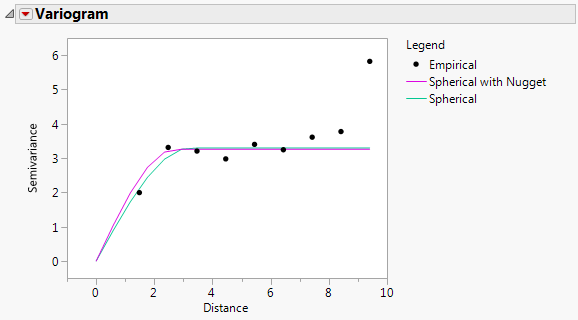
The Variogram report is shown in Fit Mixed Report - Variogram. The two variograms are virtually identical. This also suggests that there is no evidence of a nugget effect.
8.
Return to the Fit Model launch window.
9.
Select Repeated Structure tab.
10.
To test anisotropicity, select Spatial Anisotropic from the Structure list.
11.
Select Spherical from the Type list.
12.
Click Run.
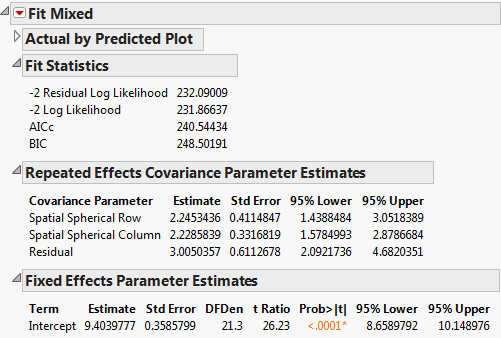
The Fit Mixed report is shown in Fit Mixed Report - Spatial Anisotropic Spherical. The fit statistics indicate not as good a fit as the isotropic (spatial structure) spherical model (AICc 240.54 compared to 234.08). The Repeated Effects Covariance Parameter Estimates report shows that the estimates for the Row (Spatial Spherical Row) and Column (Spatial Spherical Column) covariances are very close. There is no evidence to suggest that spatial correlations within rows and columns of the grid differ.
Fit Mixed Report - Spatial Anisotropic Spherical
Determine the Type of the Spatial Structure
An isotropic spatial structure with no nugget is appropriate. To determine the Type of the spatial structure, you can compare the available types.
Repeat step 1 through step 4 in Select the Type of Spatial Covariance. Change Spatial with Nugget to Spatial and then change Spherical to the other available types: Power, Exponential, Gaussian. The observed AICc values for these types and the other fits that you performed are summarized in Fit Statistics for Spatial Models Fit.
Fit Statistics for Spatial Models Fit 
Structure
Type
AICc
BIC
Spatial
Spherical
234.08
240.16
Residual
258.41
262.53
Spatial with Nugget
Spherical
236.36
244.31
Spatial Anisotropic
Spherical
240.54
248.50
Spatial
Power
240.24
246.32
Spatial
Exponential
240.24
246.32
Spatial
Gaussian
238.37
244.44
The best fitting spatial model is the Spherical covariance structure. Now you must compare this model to the complete and incomplete block models to complete the objectives of the uniformity trial.
Compare the Model to Block Designs
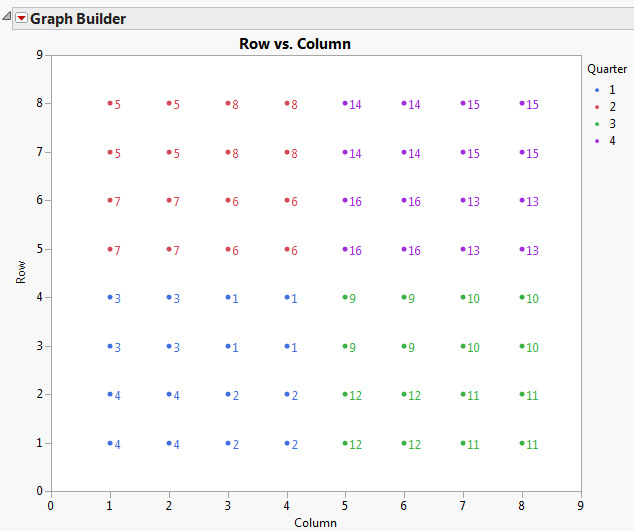
Run the Graph Builder script from the Uniformity Trial.jmp sample data table. Graph Builder Plot of Proposed Complete and Incomplete Block Designs shows the plot of the proposed complete and incomplete block designs for the field. The color indicates the quarter fields that would serve as complete blocks. The numbered points represent the subquarter fields that would serve as incomplete blocks.
Graph Builder Plot of Proposed Complete and Incomplete Block Designs
To fit the complete block model, follow these steps.
1.
Return to the Fit Model launch window.
2.
Select Repeated Structure tab.
3.
Select Residual from the Structure list.
4.
Remove Row and Col from the effect. Otherwise, a pop-up dialog appears, stating, “Repeated columns and subject columns are ignored when the Residual covariance structure is selected.”
5.
Select the Random Effects tab.
6.
Select Quarter and click Add.
7.
Click Run.
8.
Run the incomplete block model by replacing Quarter in step 6 with Subquarter.
Both AICc’s and BICs for the competing models are shown in Fit Statistics for Spatial and Block Models. The spherical covariance structure results in the best model fit. This indicates that, for future studies using this field, a completely randomized design with spatially correlated errors is preferred.
Fit Statistics for Spatial and Block Models 
Model
AICc
BIC
Spherical
234.08
240.16
RCBD
259.90
265.97
Incomplete block
248.77
254.85
Correlated Response Example
Consider the Tiretread Stacked.jmp sample data table. The effect of three factors (Silica, Silane, and Sulfur) is studied for four responses (Abrasion, Modulus, Elong, and Hardness).
Open Tiretread.jmp to see a format that is typically used for recording repeated measures data. For Mixed Model analysis of this data, each repeated measurement needs to be in its own row, as in Tiretread Stacked.jmp. To construct Tiretread Stacked.jmp, the data in Tiretread.jmp was stacked using Tables > Stack.
One way to analyze this data is to fit separate response surfaces for each of the four responses. This modeling approach assumes that the responses are independent. However, all four measurements are taken on each tire, so it is possible that there is within-tire correlation. Failure to account for this correlation could result in poor decisions and predictions. You can use the Mixed Model personality to account for and model the possible correlation.
You want to fit separate response surfaces for the four responses while simultaneously accounting for possible correlation among the responses.
1.
Select Help > Sample Data Library and open Tiretread Stacked.jmp.
2.
Select Analyze > Fit Model.
3.
Select Y and click Y.
4.
Select Mixed Model from the Personality list.
5.
Select Characteristic and click Add.
Characteristic creates a separate effect for each type of response measurement. This allows different intercepts for the four response surfaces.
6.
Select Silica, Silane, and Sulfur, and select Response Surface from the Macros list.
7.
Select the nine response surface effects in the Fixed Effects tab.
8.
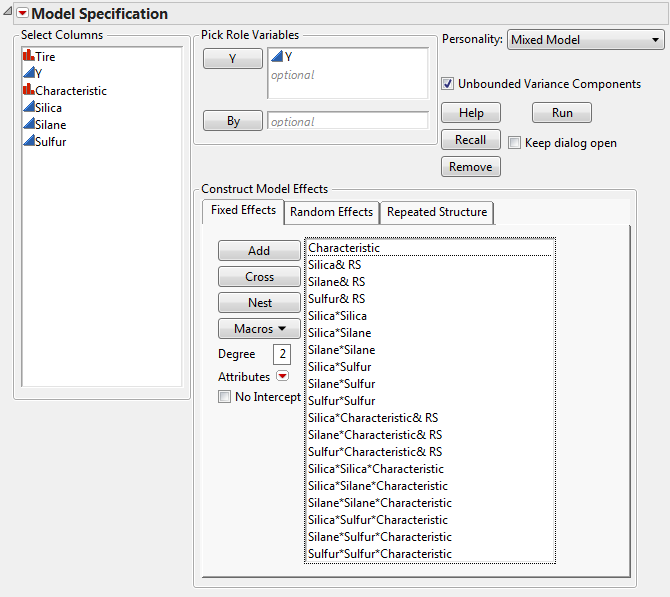
Select Characteristic from the Select Columns list.
9.
Click Cross.
This adds effects that allow individual fits for the four response surfaces.
Fit Model Launch Window Showing Completed Fixed Effects Tab shows the completed fixed effects tab.
Fit Model Launch Window Showing Completed Fixed Effects Tab
10.
Select the Repeated Structure tab.
11.
Select Unstructured from the Structure list.
12.
Select Characteristic and click Repeated.
13.
Select Tire and click Subject.
Fit Model Launch Window Showing Repeated Structure Tab
14.
Click Run.
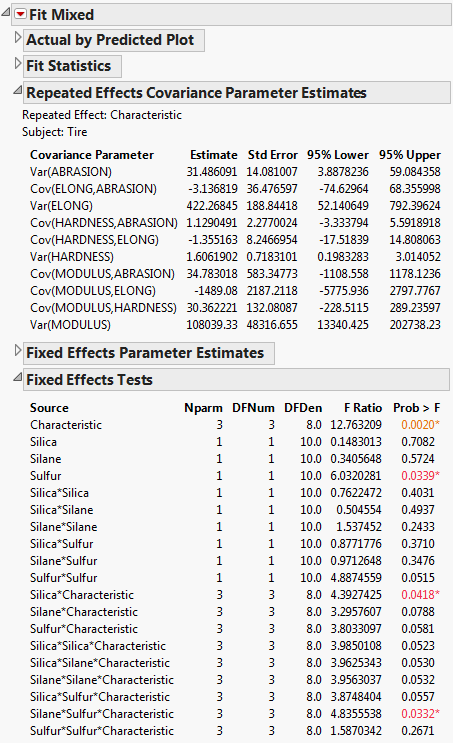
The Fit Mixed report is shown in Fit Mixed Report. The Repeated Effects Covariance Parameter Estimates report gives the estimated variances and covariances for the four responses. All of the confidence intervals for the covariance estimates include zero. This suggests that the analysis of the responses that treats them as independent is not necessarily incorrect. Although, there might not be enough data to detect nonzero covariances.
In any case, using the repeated measures approach, the model that is fit acknowledges any potential covariance among responses. More importantly, it provides additional information about effects.
The Fixed Effects Test report indicates that Characteristic is significant. This is expected. However, note that the Silane*Sulfur*Characteristic and Silica*Characteristic interactions are significant. The significance of the Silane*Sulfur*Characteristic reflects the fact that, for the usual univariate analysis, Silane*Sulfur is significant for some responses and not for others. Although Silica is significant for all responses, the significance of the Silica*Characteristic interaction suggests that Silica impacts the four responses differently.
Fit Mixed Report
Explore the Silane*Sulfur*Characteristic Interaction Using the Surface Profiler
1.
Select Marginal Model Inference > Surface Profiler from the Fit Mixed red triangle menu.
2.
In the Independent Variables panel, select Silane and Sulfur.
The values of the Characteristic column are represented by 0 (ABRASION), 1 (ELONG), 2 (HARDNESS), and 3 (MODULUS). (These values are determined by the column’s value ordering.)
3.
Change the Characteristic value to 3 for MODULUS (Surface Profiler Showing the Response Surface for MODULUS and Silica = 1.2).
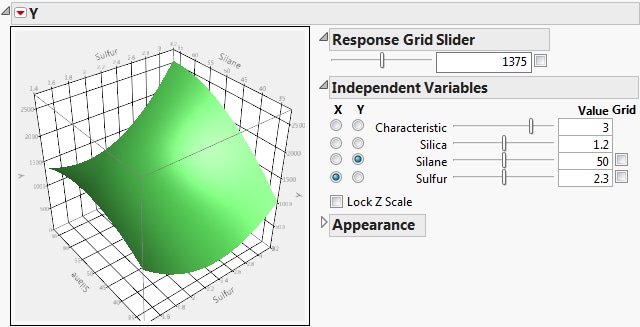
Note that Surface Profiler Showing the Response Surface for MODULUS and Silica = 1.2 shows a cross-section of the response surface for the Silica value 1.2.
Surface Profiler Showing the Response Surface for MODULUS and Silica = 1.2
Explore Interactions Using the Profiler
1.
Select Marginal Model Inference > Profiler from the Fit Mixed red triangle menu.
2.
Move the red dashed vertical line in the Characteristic panel through all four Characteristics as you view the other factors.
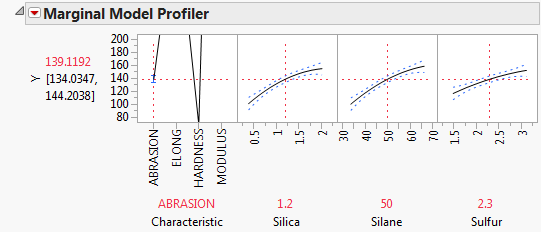
The predicted values shown in the profiler match those obtained using the univariate analysis. However, the model includes effects that involve Characteristic. This makes it easier for you to identify the impact of the operational factors. Profiler for the Correlated Tire Tread Analysis shows the profiler for ABRASION. The Y scale is changed to display the effects of Silica, Silane, and Sulfur more effectively.
Profiler for the Correlated Tire Tread Analysis