Reliability and Survival Methods • Fit Parametric Survival • Additional Examples of Fitting Parametric Survival
Previous
 • 
Next
Additional Examples of Fitting Parametric Survival
This section contains additional examples using the Fit Parametric Survival platform.
Arrhenius Accelerated Failure LogNormal Model
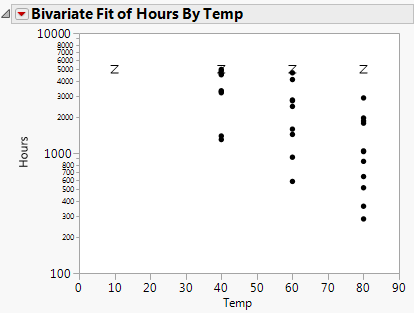
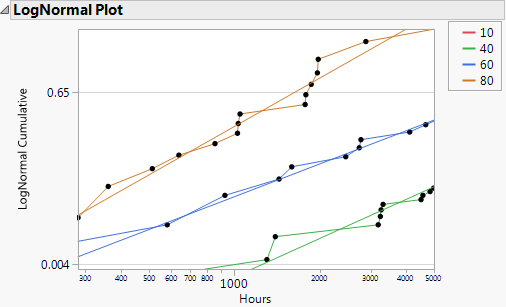
In the Devalt.jmp data, units are stressed by heating, in order to make them fail soon enough to obtain enough failures to fit the distribution.
Note: The data in Devalt.jmp comes from Meeker & Escobar (1998, p. 493).
1.
Select Help > Sample Data Library and open Reliability/Devalt.jmp.
First, use the Bivariate platform to see a plot of hours by temperature using the log scale for time.
2.
Select Analyze > Fit Y by X.
3.
Select Hours and click Y, Response.
4.
Select Temp and click X, Factor.
5.
Click OK.
Bivariate Plot of Hours by Log Temp
Next, use the survival platform to produce a LogNormal plot of the data for each temperature.
6.
Select Analyze > Reliability and Survival > Survival.
7.
Select Hours and click Y, Time to Event.
8.
Select Censor and click Censor.
9.
Select Temp and click Grouping.
10.
Select Weight and click Freq.
11.
Click OK.
12.
From the red triangle menu, select LogNormal Plot and LogNormal Fit.
Lognormal Plot
Next, use the Fit Parametric Survival platform to fit one model using a regressor for temperature.
13.
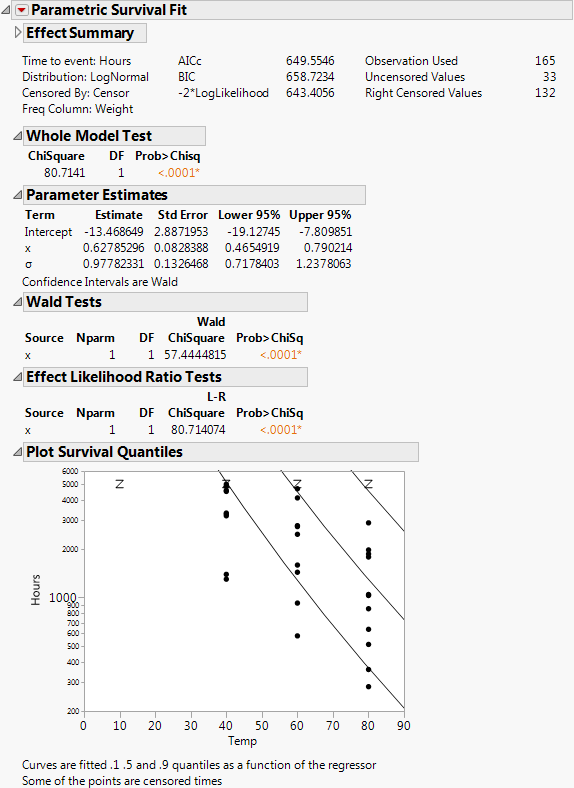
Select Analyze > Reliability and Survival > Fit Parametric Survival.
14.
Select Hours and click Time to Event.
15.
Select x and click Add.
16.
Select Censor and click Censor.
17.
Select Weight and click Freq.
18.
Change the Distribution type to Lognormal.
19.
Click Run.
Devalt Parametric Output
The result shows the regression fit of the data:
‒
If there is only one regressor and it is continuous, then a plot of the survival as a function of the regressor is shown. Lines are at 0.1, 0.5, and 0.9 survival probabilities.
‒
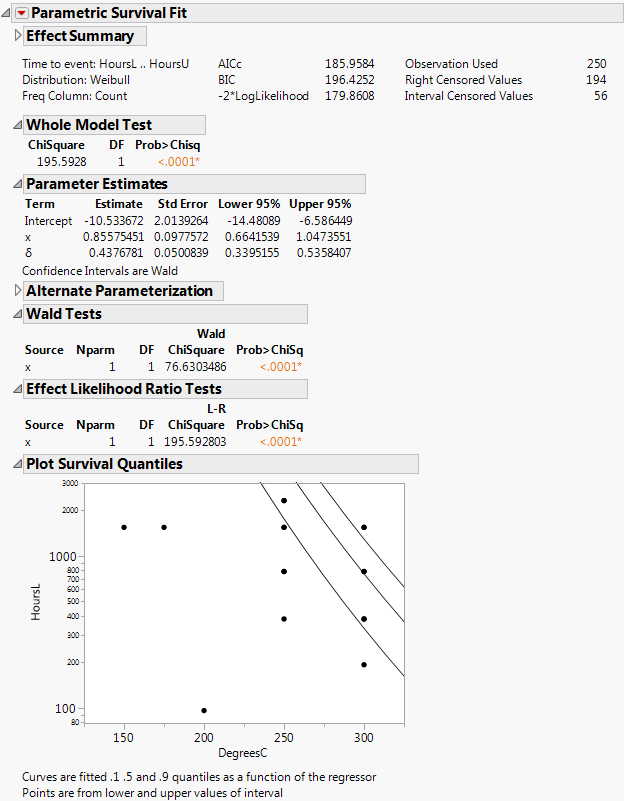
If the regressor column has a formula in terms of one other column, as in this case, the plot is done with respect to the inner column. In this case, the regressor was the column x, but the plot is done with respect to Temp, of which x is a function.
Finally, get estimates of survival probabilities extrapolated to a temperature of 10 degrees celsius for the times 30000 and 10000 hours.
20.
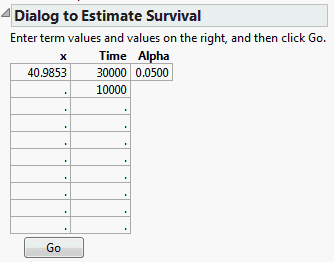
From the red triangle menu, select Estimate Survival Probability.
21.
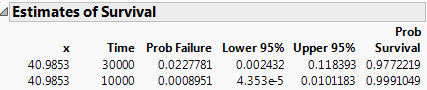
Enter the values shown in Estimating Survival Probabilities into the Dialog to Estimate Survival.
The Arrhenius transformation of 10 degrees is 40.9853, the regressor value.
Estimating Survival Probabilities
22.
Click Go.
Survival Probabilities
The Estimates of Survival report shows the estimates and a confidence interval.
Interval-Censored Accelerated Failure Time Model
The ICdevice02.jmp data shows failures that were found to have happened between inspection intervals. The model uses two y-variables, containing the upper and lower bounds on the failure times. Right-censored times are shown with missing upper bounds.
Note: The data in ICdevice02.jmp comes from Meeker & Escobar (1998, p. 640).
1.
Select Help > Sample Data Library and open Reliability/ICdevice02.jmp.
2.
Select Analyze > Reliability and Survival > Fit Parametric Survival.
3.
Select HoursL and HoursU and click Time to Event.
4.
Select Count and click Freq.
5.
Select x and click Add.
6.
Click Run.
ICDevice Output
The resulting regression shows a plot of time by degrees.
Analyze Censored Data Using the Nonlinear Platform
You can analyze left-censored data using the Nonlinear platform. For the left-censored data, zero is the censored value because it also represents the smallest known time for an observation.
Note: The Tobit model is popular in economics for responses that must be positive or zero, with zero representing a censor point.
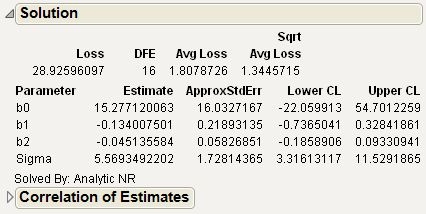
Note the following about the Tobit2.jmp data table:
•
The response variable is a measure of the durability of a product and cannot be less than zero (Durable, is left-censored at zero).
•
Age and Liquidity are independent variables.
•
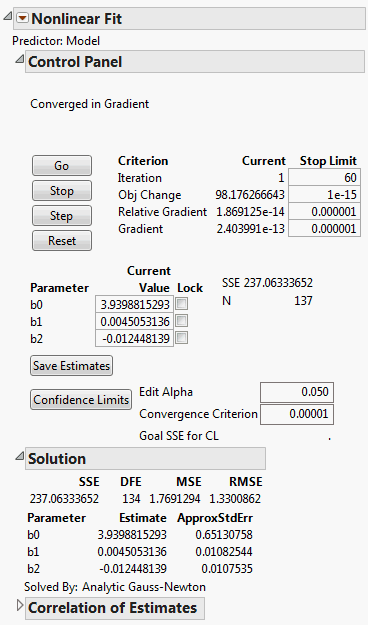
The table also includes the model and tobit loss function. The model in residual form is durable-(b0+b1*age+b2*liquidity). To see the formula associated with Tobit Loss, right-click on the column and select Formula.
Proceed as follows:
1.
Select Help > Sample Data Library and open Reliability/Tobit2.jmp.
2.
Select Analyze > Modeling > Nonlinear.
3.
Select Model and click X, Predictor Formula.
4.
Select Tobit Loss and click Loss.
5.
Click OK.
6.
Click Go.
7.
Click Confidence Limits.
Solution Report
Right-Censored Data
The Tobit model is normal, truncated at zero. However, you can take the exponential of the response and set up the intervals for a right-censored problem.
1.
Select Help > Sample Data Library and open Reliability/Tobit2.jmp.
2.
Select Analyze > Reliability and Survival > Fit Parametric Survival.
3.
Select YLow and YHigh and click Time to Event.
4.
Select age and liquidity and click Add.
5.
Change the Distribution type to Lognormal.
6.
Click Run.
Tobit Model Results
The report estimates the lognormal model fit.
Weibull Loss Function Using the Nonlinear Platform
In this example, models are fit to the survival time using the Weibull, lognormal, and exponential distributions. Model fits include a simple survival model containing only two regressors, a more complex model with all the regressors and some covariates, and the creation of dummy variables for the covariate Cell Type to be included in the full model.
Nonlinear model fitting is often sensitive to the initial values you give to the model parameters. In this example, one way to find reasonable initial values is to first use the Nonlinear platform to fit only the linear model. When the model converges, the solution values for the parameters become the initial parameter values for the nonlinear model.
1.
Select Help > Sample Data Library and open VA Lung Cancer.jmp.
The first model and all the loss functions have already been created as formulas in the data table. The Model column has the following formula:
Log(:Time) - (b0 + b1 * Age + b2 * Diag Time)
2.
Select Analyze >Modeling >  Nonlinear.
3.
Select Model and click X, Predictor Formula.
4.
Click OK.
5.
Click Go.
Initial Parameter Values in the Nonlinear Fit Control Panel
The report computes the least squares parameter estimates for this model.
6.
Click Save Estimates.
The parameter estimates in the column formulas are set to those estimated by this initial nonlinear fitting process.
The Weibull column contains the Weibull formula, explained in Weibull Loss Function.
To continue with the fitting process:
7.
Select Analyze >Modeling >  Nonlinear again.
8.
Select Model and click X, Predictor Formula.
9.
Select Weibull loss and click Loss.
10.
Click OK.
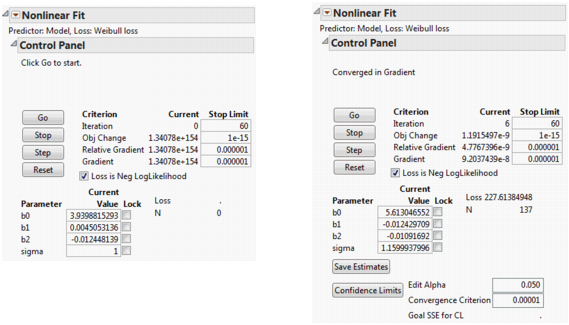
The Nonlinear Fit Control Panel on the left in Nonlinear Model with Custom Loss Function appears. There is now the additional parameter called sigma in the loss function. Because it is in the denominator of a fraction, a starting value of 1 is reasonable for sigma. When using any loss function other than the default, the Loss is Neg LogLikelihood box on the Control Panel is checked by default.
11.
Click Go.
The fitting process converges as shown on the right in Nonlinear Model with Custom Loss Function.
Nonlinear Model with Custom Loss Function
The fitting process estimates the parameters by maximizing the negative log of the Weibull likelihood function.
12.
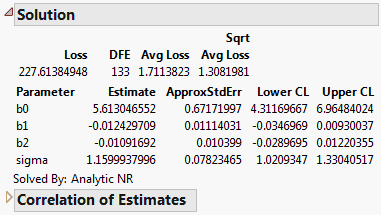
(Optional) Click Confidence Limits to show lower and upper 95% confidence limits for the parameters in the Solution table.
Solution Report
Note: Because the confidence limits are profile likelihood confidence intervals instead of the standard asymptotic confidence intervals, they can take time to compute.
You can also run the model with the predefined exponential and lognormal loss functions. Before you fit another model, reset the parameter estimates to the least squares estimates, as they might not converge otherwise. To reset the parameter estimates:
13.
(Optional) From the red triangle menu next to Nonlinear Fit, select Revert to Original Parameters.
Fitting Simple Survival Distributions Using the Nonlinear Platform
The following examples show how to use maximum likelihood methods to estimate distributions from time-censored data when there are no effects other than the censor status.
The Loss Function Templates folder has templates with formulas for exponential, extreme value, loglogistic, lognormal, normal, and one-and two-parameter Weibull loss functions. To use these loss functions, copy your time and censor values into the Time and censor columns of the loss function template. To run the model, select Nonlinear and assign the loss column as the Loss variable. Because both the response model and the censor status are included in the loss function and there are no other effects, you do not need a prediction column (model variable).
Exponential, Weibull, and Extreme-Value Loss Function
The Fan.jmp data table can be used to illustrate the Exponential, Weibull, and Extreme value loss functions discussed in Nelson (1982). The data are from a study of 70 diesel fans that accumulated a total of 344,440 hours in service. The fans were placed in service at different times. The response is failure time of the fans or run time, if censored.
Tip: To view the formulas for the loss functions, in the Fan.jmp data table, right-click the Exponential, Weibull, and Extreme value columns and select Formula.
1.
Select Help > Sample Data Library and open Reliability/Fan.jmp.
2.
Select Analyze > Modeling > Nonlinear.
3.
Select Exponential and click Loss.
4.
Click OK.
5.
Make sure that the Loss is Neg LogLikelihood check box is selected.
6.
Click Go.
7.
Click Confidence Limits.
8.
Repeat these steps, selecting Weibull and Extreme value instead of Exponential.
Nonlinear Fit Results
Lognormal Loss Function
The Locomotive.jmp data can be used to illustrate a lognormal loss. The lognormal distribution is useful when the range of the data is several powers of e.
Tip: To view the formula for the loss function, in the Locomotive.jmp data table, right-click on the logNormal column and select Formula.
The lognormal loss function can be very sensitive to starting values for its parameters. Because the lognormal distribution is similar to the normal distribution, you can create a new variable that is the natural log of Time and use Distribution to find the mean and standard deviation of this column. Then, use those values as starting values for the Nonlinear platform. In this example, the mean of the natural log of Time is 4.72 and the standard deviation is 0.35.
1.
Select Help > Sample Data Library and open Reliability/Locomotive.jmp.
2.
Select Analyze > Modeling > Nonlinear.
3.
Select logNormal and click Loss.
4.
Click OK.
5.
Click Go.
6.
Click Confidence Limits.
Solution Report
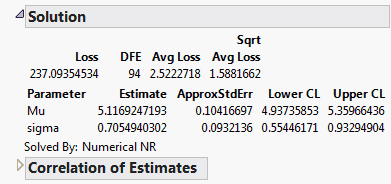
The maximum likelihood estimates of the lognormal parameters are 5.11692 for Mu and 0.7055 for Sigma (in natural logs). The corresponding estimate of the median of the lognormal distribution is the antilog of 5.11692 (e5.11692), which is approximately 167. This represents the typical life for a locomotive engine.