A market research study was undertaken to evaluate preference for a brand of detergent (Ries and Smith 1963). The results are in the Detergent.jmp sample data table. The model is defined by the following:
|
•
|
the response variable, brand with values m and x
|
|
•
|
an effect called softness (water softness) with values soft, medium, and hard
|
|
•
|
an effect called previous use with values yes and no
|
|
•
|
an effect called temperature with values high and low
|
|
•
|
a count variable, count, which gives the frequency counts for each combination of effect categories.
|
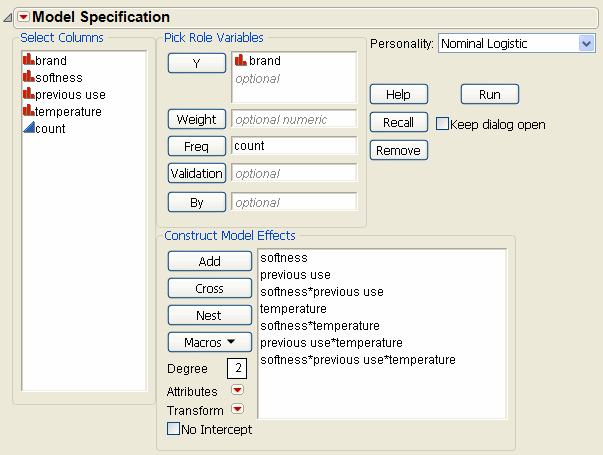
The study begins by specifying the full three-factor factorial model as shown by the Fit Model dialog in A Three-Factor Factorial Model with Nominal Response. To specify a factorial model, highlight the three main effects in the column selector list. Then select Full Factorial from the Macros popup menu.
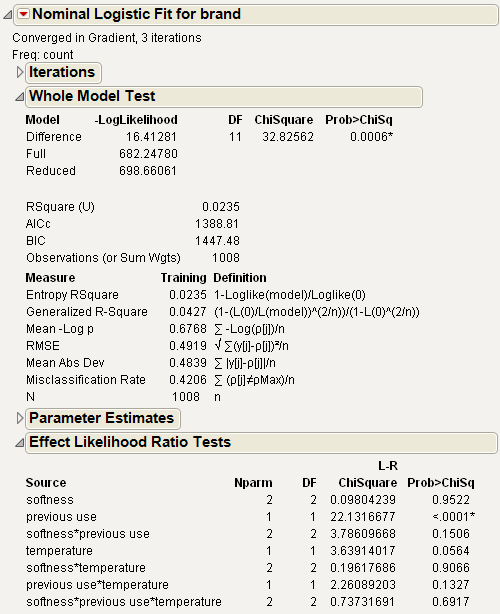
The tables in Tables for Nominal Response Three-Factor Factorial show the three-factor model as a whole to be significant (Prob>ChiSq = 0.0006) in the Whole Model table. The Effect Likelihood Ratio Tests table shows that the effects that include softness do not contribute significantly to the model fit.
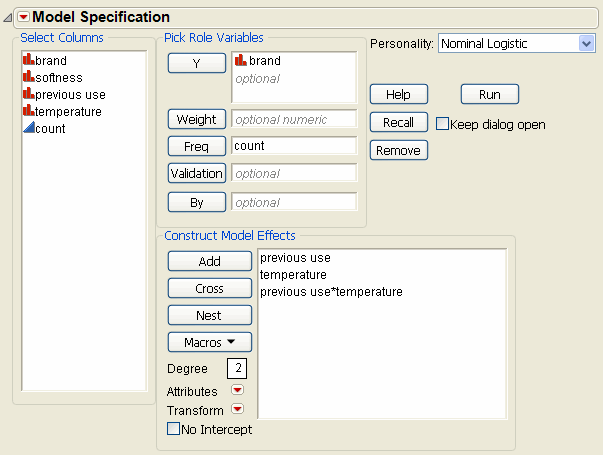
Next, use the Fit Model Dialog again to remove the softness factor and its interactions because they do not appear to be significant. You can do this easily by double-clicking the softness factor in the Fit Model dialog. A dialog appears, asking if you want to remove the other factors that involve softness (click Yes). This leaves the two-factor factorial model in A Two-factor Factorial Model with Nominal Response.
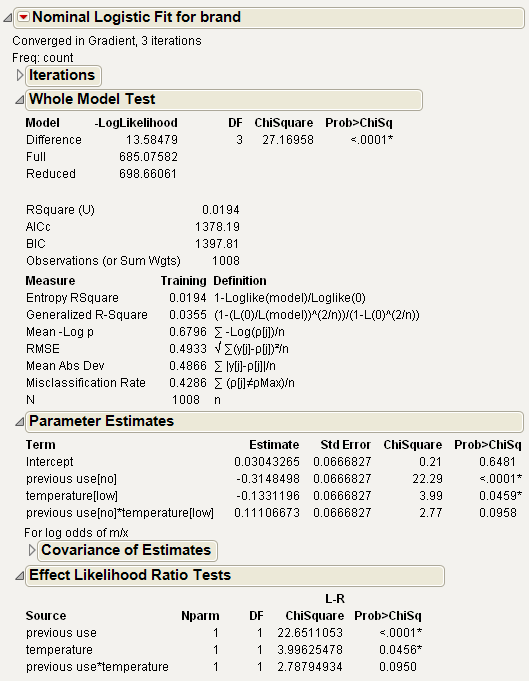
The Whole Model Test table shows that the two-factor model fits as well as the three-factor model. In fact, the three-factor Whole Model table in Tables for Nominal Response Three-Factor Factorial shows a larger Chi-square value (32.83) than the Chi-square value for the two-factor model (27.17) in the Whole Model table in Two-Factor Model. This results from the change in degrees of freedom used to compute the Chi-square values and their probabilities.
The report shown in Two-Factor Model supports the conclusion that previous use of a detergent brand, and water temperature, have an effect on detergent preference, and the interaction between temperature and previous use is not statistically significant (the effect of temperature does not depend on previous use).