The linear regression model is formulated as 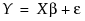 . Here X is a matrix whose first column consists of 1s, and whose remaining columns are the values of the non-intercept terms in the model. If the model consists of p terms, including the intercept, then X is an n by p matrix, where n is the number of observations. The parameter estimates, denoted by the vector b, are typically given by the formula:
. Here X is a matrix whose first column consists of 1s, and whose remaining columns are the values of the non-intercept terms in the model. If the model consists of p terms, including the intercept, then X is an n by p matrix, where n is the number of observations. The parameter estimates, denoted by the vector b, are typically given by the formula:
However, this formula presumes that 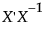 exists, in other words, that the p x p matrix
exists, in other words, that the p x p matrix 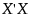 is invertible, or equivalently, of full rank. Situations often arise when
is invertible, or equivalently, of full rank. Situations often arise when 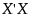 is not invertible because there are linear dependencies among the columns of X.
is not invertible because there are linear dependencies among the columns of X.
In such cases, the matrix 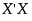 is singular, and the Fit Least Squares report displays a report entitled Singularity Details immediately below the main title bar (Singularity and Parameter Estimates Report for Model with Linear Dependencies). This report gives expressions that describe the linear dependencies. The terms involved in these linear dependencies are aliased (confounded).
is singular, and the Fit Least Squares report displays a report entitled Singularity Details immediately below the main title bar (Singularity and Parameter Estimates Report for Model with Linear Dependencies). This report gives expressions that describe the linear dependencies. The terms involved in these linear dependencies are aliased (confounded).
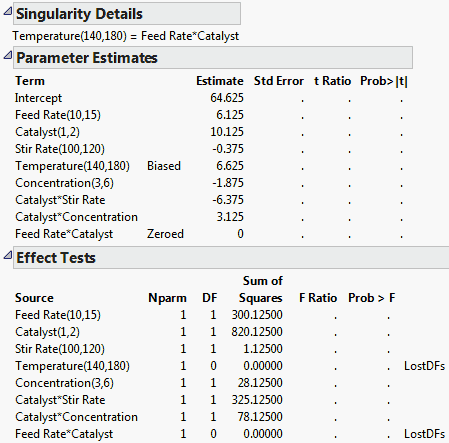
Singularity and Parameter Estimates Report for Model with Linear Dependencies shows reports for the Reactor 8 Runs.jmp sample data table. To obtain these reports, fit a model with Percent Reacted as Y. Enter Feed Rate, Catalyst, Stir Rate, Temperature, Concentration, Catalyst*Stir Rate, Catalyst*Concentration, and Feed Rate*Catalyst as model effects.
However, estimates of parameters for terms involved in linear dependencies are not unique. Because the associated terms are aliased, there are infinitely many vectors of estimates that satisfy the least squares criterion. In these cases, “Biased” appears to the left of these estimates in the Parameter Estimates report. “Zeroed” appears to the left of the estimates of 0 in the Parameter Estimates report for terms involved in a linear dependency whose parameters cannot be estimated. For an example, see Singularity and Parameter Estimates Report for Model with Linear Dependencies.
If there are degrees of freedom available for an estimate of error, t tests for parameters estimated using biased estimates are conducted. These tests should be interpreted with caution, though, given that the estimates are not unique.
An F test is conducted if the degrees of freedom for an effect are nonzero, assuming that there are degrees of freedom for error. Whenever DF is less than Nparm, the description LostDFs is displayed to the far right in the row corresponding to the effect (Singularity and Parameter Estimates Report for Model with Linear Dependencies). These effects have the opportunity to explain only model sums of squares that have not been attributed to the aliased effects that have absorbed their lost degrees of freedom. It follows that the sum of squares given in the Effect Tests report most likely underrepresents the “true” sum of squares associated with the effect. If the test is significant, its significance is meaningful. But lack of significance should be interpreted with caution.
For more details, see the section “Statistical Background” in the “Introduction to Statistical Modeling with SAS/STAT Software” chapter of the SAS/STAT 9.2 User’s Guide (2008).
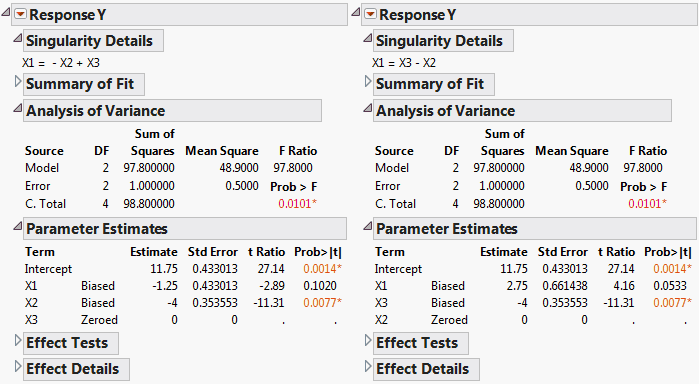
Open the Singularity.jmp sample data table. There is a response Y, four predictors X1, X2, X3, and A, and five observations. The predictors are continuous except for A, which is nominal with four levels. Also note that there is a linear dependency among the continuous effects, namely, X3 = X1 + X2.
|
1.
|
|
2.
|
Run the script Model 1. The script opens a Fit Model launch window where the effects are entered in the order X1, X2, X3.
|
|
3.
|
Click Run and leave the report window open.
|
|
4.
|
Run the script Model 2. The script opens a Fit Model launch window where the effects are entered in the order X1, X3, X2.
|
|
5.
|
Click Run and leave the report window open.
|
Compare the two reports (Fit Least Squares Reports for Model 1 (on left) and Model 2 (on right)). The Singularity Details report at the top of both reports displays the linear dependency, indicating that X1 = X3 - X2.
Now compare the Parameter Estimates reports for both models. Note, for example, that the estimate for X1 for Model 1 is –1.25 while for Model 2 it is 2.75. In both models, only two of the terms associated with effects are estimated, because there are only two model degrees of freedom. See the Analysis of Variance report. The estimates of the two terms that are estimated are labeled Biased while the remaining estimate is set to 0 and labeled Zeroed.
To gain more insight on LostDFs, follow the steps below or run the data table script Fit Model Report:
|
1.
|
|
2.
|
Click Analyze > Fit Model.
|
|
3.
|
|
4.
|
|
5.
|
|
6.
|
Click Run.
|
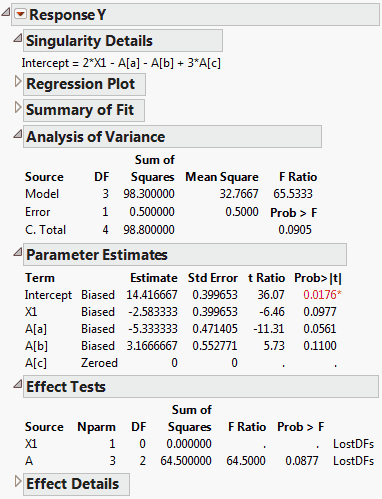
Portions of the report are shown in (Fit Least Squares Report for Model with X1 and A). The Singularity Details report shows that there is a linear dependency involving X1 and the three terms associated with the effect A. (For details about how a nominal effect is coded, see Details of Custom Test Example). The Analysis of Variance report shows that there are three model degrees of freedom. The Parameter Estimates report shows Biased estimates for the three terms X1, A[a], and A[b] and a Zeroed estimate for the fourth, A[c].
The Effect Tests report shows that X1 cannot be tested, because A must be entered first and A accounts for the three model degrees of freedom. However, A can be tested, but with only two degrees of freedom. (X1 must be entered first and it accounts for one of the model degrees of freedom.) The test for A is partial, so it must be interpreted with care.