Statistical Details

This section provides statistical details and other notes concerning the Nonlinear platform.

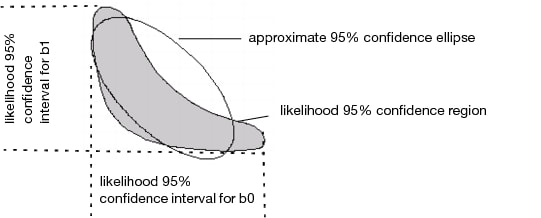
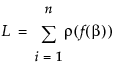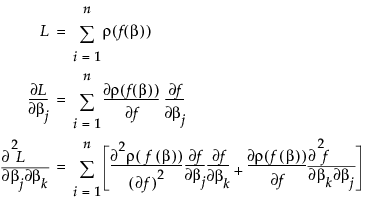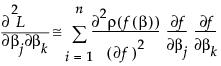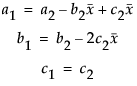The upper and lower confidence limits for the parameters are based on a search for the value of each parameter after minimizing with respect to the other parameters. The search looks for values that produce an SSE greater by a certain amount than the solution’s minimum SSE. The goal of this difference is based on the F-distribution. The intervals are sometimes called likelihood confidence intervals or profile likelihood confidence intervals (Bates and Watts 1988; Ratkowsky 1990).

Profile confidence limits all start with a goal SSE. This is a sum of squared errors (or sum of loss function) that an F test considers significantly different from the solution SSE at the given alpha level. If the loss function is specified to be a negative log-likelihood, then a Chi-square quantile is used instead of an F quantile. For each parameter’s upper confidence limit, the parameter value is increased until the SSE reaches the goal SSE. As the parameter value is moved up, all the other parameters are adjusted to be least squares estimates subject to the change in the profiled parameter. Conceptually, this is a compounded set of nested iterations. Internally there is a way to do this with one set of iterations developed by Johnston and DeLong. See SAS/STAT 9.1 vol. 3 pp. 1666-1667.

Diagram of Confidence Limits for Parameters shows the contour of the goal SSE or negative likelihood, with the least squares (or least loss) solution inside the shaded region:

•	The asymptotic standard errors produce confidence intervals that approximate the region with an ellipsoid and take the parameter values at the extremes (at the horizontal and vertical tangents).

•	Profile confidence limits find the parameter values at the extremes of the true region, rather than the approximating ellipsoid.

Diagram of Confidence Limits for Parameters

Likelihood confidence intervals are more trustworthy than confidence intervals calculated from approximate standard errors. If a particular limit cannot be found, computations begin for the next limit. When you have difficulty obtaining convergence, try the following:

•	use a larger alpha, resulting in a shorter interval, more likely to be better behaved

•	use the option for second derivatives

•	relax the confidence limit criteria.

How Custom Loss Functions Work

The nonlinear facility can minimize or maximize functions other than the default sum of squares residual. This section shows the mathematics of how it is done.

Suppose that f(β) is the model. Then the Nonlinear platform attempts to minimize the sum of the loss functions written as

The loss function

for each row can be a function of other variables in the data table. It must have nonzero first- and second-order derivatives. The default

function, squared-residuals, is

To specify a model with a custom loss function, construct a variable in the data table and build the loss function. After launching the Nonlinear platform, select the column containing the loss function as the loss variable.

The nonlinear minimization formula works by taking the first two derivatives of

with respect to the model, and forming the gradient and an approximate Hessian as follows:

is linear in the parameters, the second term in the last equation is zero. If not, you can still hope that its sum is small relative to the first term, and use

The second term is probably small if ρ is the squared residual because the sum of residuals is small. The term is zero if there is an intercept term. For least squares, this is the term that distinguishes Gauss-Newton from Newton-Raphson. In JMP, the second term is calculated only if the Second Derivative option is checked.

Note: The standard errors, confidence intervals, and hypothesis tests are correct only if least squares estimation is done, or if maximum likelihood estimation is used with a proper negative log likelihood.

Notes Concerning Derivatives

The nonlinear platform takes symbolic derivatives for formulas with most common operations. This section shows what type of derivative expressions result.

If you open the Negative Exponential.jmp nonlinear sample data example, the actual formula for the Nonlinear column looks something like this:

Parameter({b0=0.5, b1=0.5}, b0*(1-Exp(-b1*X)))

The Parameter block in the formula is hidden if you use the formula editor. That is how it is stored in the column and how it appears in the Nonlinear Launch dialog. Two parameters named b0 and b1 are given initial values and used in the formula to be fit.

The Nonlinear platform makes a separate copy of the formula, and edits it to extract the parameters from the expression. Then it maps the references to them to the place where they are estimated. Nonlinear takes the analytic derivatives of the prediction formula with respect to the parameters. If you use the Show Derivatives command, you get the resulting formulas listed in the log, like this:

Prediction Model:

b0 * First(T#1=1-(T#2=Exp(-b1*X)), T#3=-(-1*T#2*X))

The Derivative of Model with respect to the parameters is:

{T#1, T#3*b0}

The derivative facility works like this:

•	In order to avoid calculating subexpressions repeatedly, the prediction model is threaded with assignments to store the values of subexpressions that it needs for derivative calculations. The assignments are made to names like T#1, T#2, and so on.

•	When the prediction model needs additional subexpressions evaluated, it uses the First function, which returns the value of the first argument expression, and also evaluates the other arguments. In this case additional assignments are needed for derivatives.

•

The derivative table itself is a list of expressions, one expression for each parameter to be fit. For example, the derivative of the model with respect to b0 is T#1; its thread in the prediction model is 1–(Exp(-b1*X)). The derivative with respect to b1 is T#3*b0, which is –(–1*Exp(-b1*X)*X)*b0 if you substitute in the assignments above. Although many optimizations are made, it does not always combine the operations optimally. You can see this by the expression for T#3, which does not remove a double negation.

If you ask for second derivatives, then you get a list of (m(m + 1))/2 second derivative expressions in a list, where m is the number of parameters.

If you specify a loss function, then the formula editor takes derivatives with respect to parameters, if it has any. And it takes first and second derivatives with respect to the model, if there is one.

If the derivative mechanism does not know how to take the analytic derivative of a function, then it takes numerical derivatives, using the NumDeriv function. If this occurs, the platform shows the delta that it used to evaluate the change in the function with respect to a delta change in the arguments. You might need to experiment with different delta settings to obtain good numerical derivatives.

Tips

There are always many ways to represent a given model, and some ways behave much better than other forms. Ratkowsky (1990) covers alternative forms in his text.

If you have repeated subexpressions that occur several places in a formula, then it is better to make an assignment to a temporary variable. Then refer to it later in the formula. For example, one of the model formulas above was this:

If(Y==0, Log(1/(1+Exp(model))), Log(1 - 1/(1 + Exp(model))));

This could be simplified by factoring out an expression and assigning it to a local variable:

temp=1/(1+Exp(model));

If(Y==0, Log(temp), Log(1-temp));

The derivative facility can track derivatives across assignments and conditionals.

Notes on Effective Nonlinear Modeling

We strongly encourage you to center polynomials.

Anywhere you have a complete polynomial term that is linear in the parameters, it is always good to center the polynomials. This improves the condition of the numerical surface for optimization. For example, if you have an expression like

a1 + b1x + c1x2