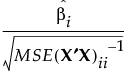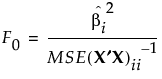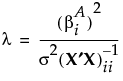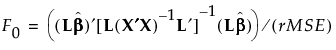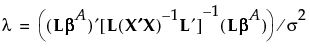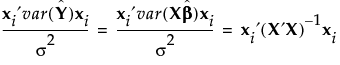The model matrix. See the Fitting Linear Models book for information on the coding for nominal effects. Also, see The Model Matrix in Technical Details.
Note: You can view the model matrix by running Fit Model. Then select Save Columns > Save Coding Table from the red triangle menu for the main report.
βi
The variance of 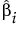 is given by the ith diagonal entry of
is given by the ith diagonal entry of 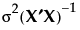 , where σ2 is the error variance. Denote the ith diagonal entry of
, where σ2 is the error variance. Denote the ith diagonal entry of 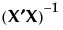 by
by 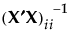 .
.
The error variance, σ2, is estimated by the MSE, and has 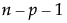 degrees of freedom, where n is the number of observations and p is the number of terms other than the intercept in the model.
degrees of freedom, where n is the number of observations and p is the number of terms other than the intercept in the model.
If the true value of 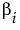 is
is 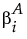 , then F0 has a noncentral F distribution with noncentrality parameter given by:
, then F0 has a noncentral F distribution with noncentrality parameter given by:
|
Matrix that defines the test for the categorical effect. The matrix L identifies the values of the parameters in β corresponding to the categorical effect and sets them equal to 0. The null hypothesis for the test of the categorical effect is given by:
|
|
Note: You can view the design matrix by running Fit Model. Then select Save Columns > Save Coding Table from the red triangle menu for the main report.
The covariance matrix of 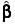 is given by
is given by 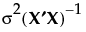 , where σ2 is the error variance.
, where σ2 is the error variance.
The error variance, σ2, is estimated by the MSE, and has 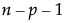 degrees of freedom, where n is the number of observations and p is the number of terms other than the intercept in the model.
degrees of freedom, where n is the number of observations and p is the number of terms other than the intercept in the model.
If the true value of β is 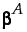 , then F0 has a noncentral F distribution with noncentrality parameter given by:
, then F0 has a noncentral F distribution with noncentrality parameter given by:
|
σ2
|
|