Additional Numeric Functions
JSL also offers several categories of operations that do not make much sense in the context of the formula editor: matrix operations and numeric derivatives of functions. Algebraic derivatives are also available.
The basic arithmetic operators can also be used with matrix arguments for matrix-wise addition, subtraction, and so on. Matrices also have a few special operators for elementwise multiplication and division, concatenation, and indexing. See Matrices in the Data Structures section.
Derivatives
JSL has three internal functions (not all available in the calculator) for taking derivatives.
Derivative() takes the first derivative of an expression with respect to names you specify in the second argument. A single name might be entered as this second argument; or multiple values can be specified in a list, in other words, surrounded by braces.
Note: Derivative() is also available as an editing command inside the formula editor (calculator), located on the drop-down list in the top center of the formula editor (above the keypad). To use it, highlight a single variable in the expression (to designate which variable the derivative should be taken with respect to), then select the Derivative command from the menu. The whole formula is replaced by its derivative with respect to the highlighted name.
In scripts, the easiest way to use the function is with a single name. In this example, we first show the mathematical notation and then the JSL equivalent.
For 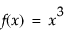 , the first derivative is f ′(x) or
, the first derivative is f ′(x) or 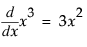 .
.
result = Derivative( x ^ 3, x );
Show( result );result = 3 * x ^ 2
If you want an efficient expression to take the derivative with respect to several variables, then the variables are specified in a list. The result is a list containing a threaded version of the original expression, followed by expressions for the derivatives. The expression is threaded by inserting assignments to temporary variables of expressions that are needed in several places for the derivatives.
Here is an example involving an expression involving three variables. Listing all three variables returns the first derivatives with respect to each. The result is a list with the original expression and then the derivatives in the order requested. However, note here that JMP creates a temporary variable T#1 for storing the subexpression x^2, and then uses that subexpression subsequently to save calculations.
result2 = Derivative( 3 * y * x ^ 2 + z ^ 3, {x, y, z} );
Show( result2 );result2 = {3 * y * (T#1 = x ^ 2) + z ^ 3, 6 * x * y, 3 * T#1, 3 * z ^ 2}
To take second derivatives, specify the variable as a third argument. Both the second and third arguments must be lists. JMP returns a list with the original expression, the first derivative(s), and then the second derivative(s) in the order requested.
second = Derivative( 3 * y * x ^ 2, {x}, {x} );
Show( second );second = {3 * y * x ^ 2, 6 * x * y, 6 * y}
second = Derivative( 3 * y * x ^ 2, {y}, {y} );
Show( second );second = {3 * y * (T#1 = x ^ 2), 3 * T#1, 0}
second = Derivative( 3 * y * x ^ 2, {y}, {x} );
Show( second );second = {3 * y * (T#2 = x ^ 2), 3 * T#2, 6 * x}
Num Deriv() takes the first numeric derivative of a function with respect to the value of the first argument by calculating the function at that value and at that value plus a small delta (Δ) and dividing the difference by the delta. Num Deriv2() computes the second numeric derivative in a similar fashion. These are used internally for nonlinear modeling but are not frequently useful in JSL. Note that these functions do not differentiate using a variable, but only with respect to arguments to a function. In order to differentiate with respect to x, you have to make x one of the immediate arguments, not a symbol buried deep into the expression.
Suppose to differentiate y = 3x2 at the value of x = 3. The incorrect way would be to submit the following script:
x = 3;n = Num Deriv( 3 * x ^ 2 );
The correct way is to make x an argument in the function.
x = 3;f = Function( {x}, 3 * x ^ 2 );
n = Num Deriv( f( x ), 1 );
18.000029999854
Consider both the mathematical notation and the JSL equivalent for another example:
For 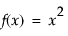 , it calculates
, it calculates 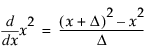 . At
. At 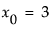 ,
, 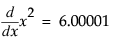 .
.
x = 3;y = Num Deriv( x ^ 2 ); // or equivalently: y = Num Deriv( 3 ^ 2 );
6.0000099999513
And here are a few more examples:
x = Num Deriv( Sqrt( 7 ) ); // returns 0.188982168980445
y = Num Deriv( Normal Distribution( 1 ) ); // returns 0.241969514669371
z = Num Deriv2( Normal Distribution( 1 ) ); // returns -0.241969777547979
Function | Syntax | Explanation |
|---|---|---|
Derivative | Derivative(expr, {name, ...}) | Returns the derivative of the expr with respect to name. Note that the second argument can be specified in a list with braces { } or simply as a variable if there is only one. Give two lists of names to take second derivatives. |
NumDeriv | NumDeriv(expr) | Returns the first numeric derivative of the expr with respect to the first argument in the expression. |
NumDeriv2 | NumDeriv2(expr) | Returns the second numeric derivative of the expr with respect to the first argument in the expression. |