Continuous Fit Distributions
This section contains statistical details for the options in the Continuous Fit menu.
Fit Normal
The Fit Normal option estimates the parameters of the normal distribution. The parameters for the normal distribution are as follows:
• μ (the mean) defines the location of the distribution on the x-axis
• σ (standard deviation) defines the dispersion or spread of the distribution
The standard normal distribution occurs when μ = 0 and σ = 1.
pdf: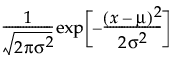 
for 
; 
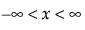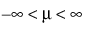; 0 < σ
E(x) = μ
Var(x) = σ2
Fit Cauchy
The Fit Cauchy option fits a Cauchy distribution with location μ and scale σ.
pdf: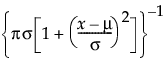 
for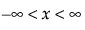 
; 
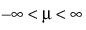; 0 < σ
E(x) = undefined
Var(x) = undefined
Fit SHASH
The Fit SHASH option fits a sinh-arcsinh (SHASH) distribution. The SHASH distribution is based on a transformation of the normal distribution and includes the normal distribution as a special case. It can be symmetric or asymmetric. The shape is determined by the two shape parameters, γ and δ. For more information about the SHASH distribution, see Jones and Pewsey (2009).
pdf: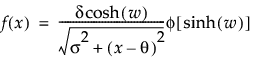 
for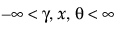 
; 0 < δ, σ
where
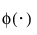is the standard normal pdf
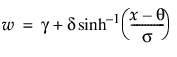
• When γ = 0 and δ = 1, the SHASH distribution is equivalent to the normal distribution with location θ and scale σ.
• The transformation sinh(w) is normally distributed with μ = 0 and σ = 1.
Fit Exponential
The exponential distribution is especially useful for describing events that randomly occur over time, such as survival data. The exponential distribution might also be useful for modeling elapsed time between the occurrence of non-overlapping events. Examples of non-overlapping events include the following: the time between a user’s computer query and response of the server, the arrival of customers at a service desk, or calls coming in at a switchboard.
The Exponential distribution is a special case of the two-parameter Weibull when β = 1 and α = σ, and also a special case of the Gamma distribution when α = 1.
pdf: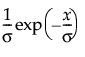 
for 0 < σ; 0 ≤ x
E(x) = σ
Var(x) = σ2
Devore (1995) notes that an exponential distribution is memoryless. Memoryless means that if you check a component after t hours and it is still working, the distribution of additional lifetime (the conditional probability of additional life given that the component has lived until t) is the same as the original distribution.
Fit Gamma
The Fit Gamma option estimates the gamma distribution parameters, α > 0 and σ > 0. The parameter α, called alpha in the fitted gamma report, describes shape or curvature. The parameter σ, called sigma, is the scale parameter of the distribution. The data must be greater than zero.
pdf: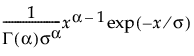 
for 0 < x; 0 < α,σ
E(x) = ασ
Var(x) = ασ2
• The standard gamma distribution has σ = 1. Sigma is called the scale parameter because values other than 1 stretch or compress the distribution along the horizontal axis.
• The Chi-square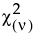 
distribution occurs when σ = 2 and α = ν/2.
• The exponential distribution occurs when α = 1.
The standard gamma density function is strictly decreasing when α ≤ 1. When α > 1, the density function begins at zero, increases to a maximum, and then decreases.
Fit Lognormal
The Fit Lognormal option estimates the parameters μ (scale) and σ (shape) for the two-parameter lognormal distribution. A variable Y is lognormal if and only if X = ln(Y) is normal. The data must be greater than zero.
pdf: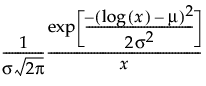 
for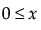 
; 
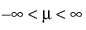; 0 < σ
E(x) =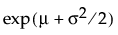 
Var(x) =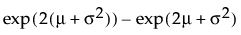 
Fit Weibull
The Weibull distribution has different shapes depending on the values of α (scale) and β (shape). It often provides a good model for estimating the length of life, especially for mechanical devices and in biology.
The pdf for the Weibull distribution is as follows:
pdf: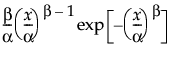 
for α,β > 0; 0 < x
E(x) =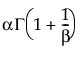 
Var(x) =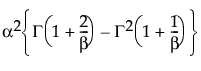 
where Γ(·) is the Gamma function.
Fit Normal 2 Mixture and Fit Normal 3 Mixture
The Fit Normal 2 Mixture and Fit Normal 3 Mixture options fit a mixture of two or three normal distributions. These flexible distributions are capable of fitting bimodal or multi-modal data. A separate mean, standard deviation, and proportion of the whole is estimated for each group. In the following equations, k equals the number of normal distributions in the mixture.
pdf: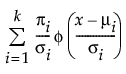 
E(x) =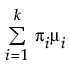
Var(x) =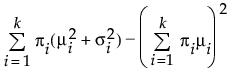
where μi, σi, and πi are the respective mean, standard deviation, and proportion for the ith group, and φ(·) is the standard normal pdf.
Fit Johnson
The Fit Johnson option selects and fits the best-fitting distribution from the Johnson system of distributions, which contains three distributions that are all based on a transformed normal distribution. These three distributions are the following:
• Johnson Su, which is unbounded.
• Johnson Sb, which has bounds on both tails. The bounds are defined by parameters that can be estimated.
• Johnson Sl, which is bounded in one tail. The bound is defined by a parameter that can be estimated. The Johnson Sl family contains the family of lognormal distributions.
Only the fit for the selected distribution is reported. Information about selection procedures and parameter estimation for the Johnson distributions can be found in Slifker and Shapiro (1980). The parameter estimation does not use maximum likelihood.
Johnson distributions are popular because of their flexibility. In particular, the Johnson distribution system is noted for its data-fitting capabilities because it supports every possible combination of skewness and kurtosis. However, the SHASH distribution is also very flexible and is recommended over the Johnson distributions.
If Z is a standard normal variate, then the system is defined as follows:
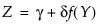
where, for the Johnson Su:
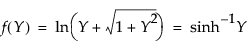
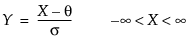
where, for the Johnson Sb:
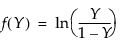
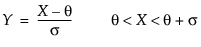
and for the Johnson Sl, where σ = ±1.
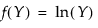
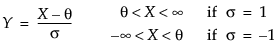
Johnson Su
pdf: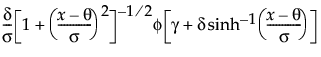 
for -∞ < x, θ, γ < ∞; 0 < θ,δ
Johnson Sb
pdf: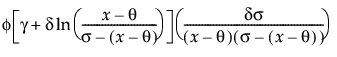 
for θ < x < θ+σ; 0 < σ
Johnson Sl
pdf: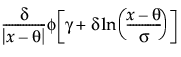 
for θ < x if σ = 1; θ > x if σ = -1
where φ(·)is the standard normal pdf.
Fit Beta
The beta distribution is useful for modeling the behavior of random variables that are constrained to fall in the interval 0,1. For example, proportions always fall between 0 and 1. The Fit Beta option estimates two shape parameters, α > 0 and β > 0. The beta distribution has values only in the interval 0,1.
pdf: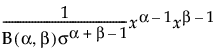 
for 0 < x < 1; 0 < σ,α,β
E(x) =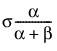 
Var(x) =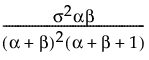 
where B(·) is the Beta function.
Fit All
In the Compare Distributions report, the Distribution list is sorted by AICc in ascending order.
The formulas for AICc and BIC are as follows:
AICc =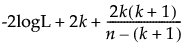 
BIC =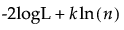 
where:
– logL is the log-likelihood.
– n is the sample size.
– k is the number of parameters.
The AICc Weight column shows normalized AICc values that sum to one. The AICc weight can be interpreted as the probability that a particular distribution is the true distribution given that one of the fitted distributions is the truth. Therefore, the distribution with the AICc weight closest to one is the better fit. The AICc weights are calculated using only nonmissing AICc values, as follows:
AICcWeight = exp[-0.5(AICc-min(AICc))] / sum(exp[-0.5(AICc-min(AICc))])
where min(AICc) is the smallest AICc value among the fitted distributions.
For more information about the measures in the Compare Distributions report, see Likelihood, AICc, and BIC in Fitting Linear Models.