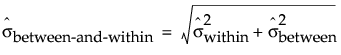Control Limits for Three Way Control Charts
Within Sigma Based on Average of Ranges
The within sigma estimate for three way control charts that is estimated using the average of ranges can be used for the Individual on Means, Moving Range on Means and R chart.
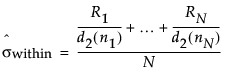
The formula uses the following notation:
Ri = range of ith subgroup
ni = sample size of ith subgroup
d2(ni) = expected value of the range of ni independent normally distributed variables with unit standard deviation
N = number of subgroups for which ni ≥ 2
Within Sigma Based on Average of Unbiased Standard Deviations
The within sigma estimate for three way control charts that is estimated using the average of unbiased standard deviations can be used for the Individual on Means, Moving Range on Means, and S chart.
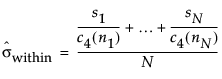
The formula uses the following notation:
si = sample standard deviation of the ith subgroup
ni = sample size of ith subgroup
c4(ni) = expected value of the standard deviation of ni independent normally distributed variables with unit standard deviation
N = number of subgroups for which ni ≥ 2
Between Sigma
The between sigma estimate for three way control charts is estimated using the moving range of subgroup means.
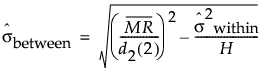
The formula uses the following notation:
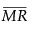 = the mean of the nonmissing moving ranges computed as (MR2+MR3+...+MRN)/(N-1) where MRi = |yi - yi-1|.
= the mean of the nonmissing moving ranges computed as (MR2+MR3+...+MRN)/(N-1) where MRi = |yi - yi-1|.
d2(2) = expected value of the range of two independent normally distributed variables with unit standard deviation.
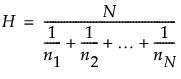 , the harmonic mean of subgroup sample sizes.
, the harmonic mean of subgroup sample sizes.
Note: If between Sigma is estimated as a negative value, it is set to 0.
Between-and-Within Sigma
The between-and-within sigma estimate for three way control charts is estimated using a combination of the within sigma and between sigma estimates.