Estimation Methods

REML

REML (restricted maximum likelihood) estimates are less biased than the ML (maximum likelihood) estimation method when the data contains missing values. The REML method maximizes marginal likelihoods based on error contrasts. The REML method is often used for estimating variances and covariances. The REML method in the Principal Components platform is the same as the REML estimation of mixed models for repeated measures data with an unstructured covariance matrix. See the documentation for SAS PROC MIXED (2017f) about REML estimation of mixed models.

Robust

This method essentially ignores any outlying values by substantially down-weighting them. A sequence of iteratively reweighted fits of the data is done using the following weight:

wi = 1.0 if Q < K and wi = K/Q otherwise

Here, K is a constant equal to the 0.75 quantile of a chi-square distribution with the degrees of freedom equal to the number of columns in the data table. Q is defined as follows:

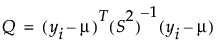
In this equation, yi = the response for the ith observation, μ = the current estimate of the mean vector, S2 = current estimate of the covariance matrix, and T = the transpose matrix operation. The final step is a bias reduction of the variance matrix.

The trade off of this method is that you can have higher variance estimates when the data do not have many outliers, but can have a much more precise estimate of the variances when the data do have outliers.