Partial Least Squares
Partial least squares fits linear models based on linear combinations, called factors, of the explanatory variables (Xs). These factors are obtained in a way that attempts to maximize the covariance between the Xs and the response or responses (Ys). In this way, PLS exploits the correlations between the Xs and the Ys to reveal underlying latent structures. The factors address the combined goals of explaining response variation and predictor variation. Partial least squares is particularly useful when you have more X variables than observations or when the X variables are highly correlated.
NIPALS
The NIPALS method works by extracting one factor at a time. Let X = X0 be the centered and scaled matrix of predictors and Y = Y0 the centered and scaled matrix of response values. The PLS method starts with a linear combination t = X0w of the predictors, where t is called a score vector and w is its associated weight vector. The PLS method predicts both X0 and Y0 by regression on t:
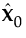 = tp′, where p´ = (t´t)-1t´X0
= tp′, where p´ = (t´t)-1t´X0
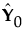 = tc´, where c´ = (t´t)-1t´Y0
= tc´, where c´ = (t´t)-1t´Y0
The vectors p and c are called the X- and Y-loadings, respectively.
The specific linear combination t = X0w is the one that has maximum covariance t´u with some response linear combination u = Y0q. Another characterization is that the X- and Y-weights, w and q, are proportional to the first left and right singular vectors of the covariance matrix X0´Y0. Or, equivalently, the first eigenvectors of X0´Y0Y0´X0 and Y0´X0X0´Y0 respectively.
This accounts for how the first PLS factor is extracted. The second factor is extracted in the same way by replacing X0 and Y0 with the X- and Y-residuals from the first factor:
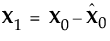
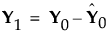
These residuals are also called the deflated X and Y blocks. The process of extracting a score vector and deflating the data matrices is repeated for as many extracted factors as desired.
SIMPLS
The SIMPLS algorithm was developed to optimize a statistical criterion: it finds score vectors that maximize the covariance between linear combinations of Xs and Ys, subject to the requirement that the X-scores are orthogonal. Unlike NIPALS, where the matrices X0 and Y0 are deflated, SIMPLS deflates the cross-product matrix, X0´Y0.
In the case of a single Y variable, these two algorithms are equivalent. However, for multivariate Y, the models differ. SIMPLS was suggested by De Jong (1993).