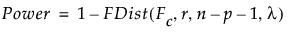Power for a Categorical Effect
This section describes how power for the test for a whole categorical effect is computed. Use the following notation:
X
Model matrix. See The Alias Matrix in the Technical Details section.
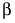
Vector of parameters.
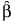
Least squares estimate of β.
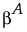
Vector of Anticipated Coefficient values.
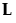
Matrix that defines the test for the categorical effect. The matrix L identifies the values of the parameters in β corresponding to the categorical effect and sets them equal to 0. The null hypothesis for the test of the categorical effect is given by:
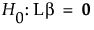
r
Rank of L. Alternatively, r is the number of levels of the categorical effect minus one.
Note: You can view the design matrix by running Fit Model. Then select Save Columns > Save Coding Table from the red triangle menu for the main report.
The covariance matrix of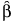 
is given by 
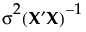, where σ2 is the error variance.
The error variance, σ2, is estimated by the MSE, and has n − p − 1 degrees of freedom, where n is the number of observations and p is the number of terms other than the intercept in the model.If n − p − 1 = 0, then JMP sets the degrees of freedom for the error to 1. This allows the power to be estimated for parameters in a saturated design.
The test of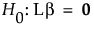 
is given by:
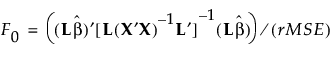
Under the null hypothesis, the test statistic F0 has an F distribution on r and n − p − 1 degrees of freedom.
If the true value of β is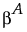 
, then F0 has a noncentral F distribution with noncentrality parameter given by:
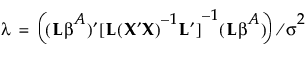
To compute the power of the test, first solve for the α-level critical value Fc:
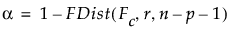
Then calculate the power as follows:
