Smoothing Models

Shows a submenu of smoothing models. Once you select a smoothing model, a specification window appears. See Smoothing Model Windows. For each model that is specified, a Smoothing Model Report appears in the report window. See Model Report. Smoothing models represent the evolution of a time series by the model:

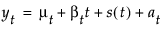
where

μt is the time-varying mean term

βt is the time-varying slope term

s(t) is one of the s time-varying seasonal terms

at are the random shocks

For more information about the general smoothing model equation, see Statistical Details for Smoothing Models. The following smoothing models are available:

Simple Moving Average

A model that estimates values by using an average of several adjacent points, defined by the smoothing window. The Simple Smoothing Average Specification window enables you to specify aspects of the smoothing window. Once specified, a Simple Moving Average report is shown. By default, this report produces plotted values that are equal to the average of consecutive observations in a time window. Multiple Simple Moving Average models can be added and shown on the same plot. See Simple Smoothing Average Specification Window.

Simple Exponential Smoothing

A model with a level component. See Simple Exponential Smoothing.

Double Exponential Smoothing

A model with a level component and a trend component. This is a special case of Linear Exponential Smoothing. See Double (Brown) Exponential Smoothing.

Linear Exponential Smoothing

A model with a level component and a trend component. See Linear (Holt) Exponential Smoothing.

Damped-Trend Linear Exponential Smoothing

A model with a level component and a damped trend component. This model is appropriate for a series that exhibits a trend more complicated than a linear trend. See Damped-Trend Linear Exponential Smoothing.

Seasonal Exponential Smoothing

A model with a level component and a seasonal component. See Seasonal Exponential Smoothing.

Winters Method

A model with a level component, a trend component, and a seasonal component. See Winters Method (Additive).

Note: Each smoothing model has an ARIMA model equivalent. You might not be able to specify the equivalent ARIMA model using the ARIMA option because some smoothing models intrinsically constrain the ARIMA model parameters in ways that the ARIMA option does not allow.