Statistical Details for V-Mask CUSUM Control Charts
The following notation is used in these formulas:
• μ denotes the mean of the population, also referred to as the process mean or the process level.
• μ0 denotes the target mean (or goal) for the population. Sometimes, the symbol 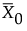 is used for μ0. See the American Society for Quality Statistics Division (2004). You can provide μ0 as the Target in the Known Statistics for CUSUM Chart area on the launch window.
is used for μ0. See the American Society for Quality Statistics Division (2004). You can provide μ0 as the Target in the Known Statistics for CUSUM Chart area on the launch window.
• σ denotes the population standard deviation. 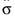 denotes an estimate of σ.
denotes an estimate of σ.
• σ0 denotes a known standard deviation. You can provide σo as the Sigma in the Known Statistics for CUSUM Chart area on the launch window.
• n denotes the nominal sample size for the CUSUM chart.
• δ denotes the shift in μ to be detected, expressed as a multiple of the standard deviation. You can provide δ as the Delta in the Known Statistics for CUSUM Chart area on the launch window.
• Δ denotes the shift in μ to be detected, expressed in data units. If the sample size n is constant across subgroups, then the following computation applies:
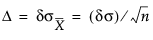
You can provide Δ as the Shift in the Known Statistics for CUSUM Chart area on the launch window.
Note: Some authors use the symbol D instead of Δ.
One-Sided CUSUM Charts
Positive Shifts
If the shift δ to be detected is positive, the CUSUM for the tth subgroup is computed as follows:
St = max(0, St – 1+ (zt – k))
t = 1, 2,..., n, where S0 = 0, zt is defined as for two-sided charts, and the parameter k, termed the reference value, is positive. If the parameter k is not specified in the launch window, k is set to δ/2. The CUSUM St is referred to as an upper cumulative sum. St can be computed as follows:
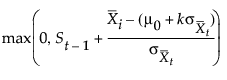
The sequence St cumulates deviations in the subgroup means greater than k standard errors from μ0. If St exceeds a positive value h (referred to as the decision interval), a shift or out-of-control condition is signaled.
Negative Shifts
If the shift to be detected is negative, the CUSUM for the tth subgroup is computed as follows:
St = max(0, St – 1 – (zt + k))
t = 1, 2,..., n, where S0 = 0, zt is defined as for two-sided charts, and the parameter k, termed the reference value, is positive. If the parameter k is not specified in the launch window, k is set to δ/2. The CUSUM St is referred to as a lower cumulative sum. St can be computed as follows:
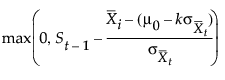
The sequence St cumulates the absolute value of deviations in the subgroup means less than k standard errors from μ0. If St exceeds a positive value h (referred to as the decision interval), a shift or out-of-control condition is signaled.
Note that St is always positive and h is always positive, regardless of whether δ is positive or negative. For charts designed to detect a negative shift, some authors define a reflected version of St for which a shift is signaled when St is less than a negative limit.
Lucas and Crosier (1982) describe the properties of a fast initial response (FIR) feature for CUSUM charts in which the initial CUSUM S0 is set to a “head start” value. Average run length calculations given by them show that the FIR feature has little effect when the process is in control and that it leads to a faster response to an initial out-of-control condition than a standard CUSUM chart. You can provide a Head Start value in the Known Statistics for CUSUM Chart area on the launch window.
Constant Sample Sizes
When the subgroup sample sizes are constant (= n), it might be preferable to compute CUSUMs that are scaled in the same units as the data. CUSUMs are then computed as follows:
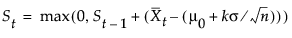
where δ > 0
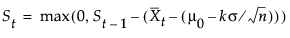
where δ < 0. In either case, the parameter k is rescaled to 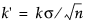 . If the parameter k is not specified in the launch window, k' is set to δ/2. A shift is signaled if St exceeds
. If the parameter k is not specified in the launch window, k' is set to δ/2. A shift is signaled if St exceeds 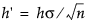 . Some authors use the symbol H for h'.
. Some authors use the symbol H for h'.
Two-Sided CUSUM Charts
If the CUSUM chart is two-sided, the cumulative sum St plotted for the tth subgroup is as follows:
St = St - 1 +zt
t = 1, 2,..., n. Here S0=0, and the term zt is calculated as follows:
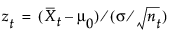
where 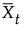 is the tth subgroup average, and nt is the tth subgroup sample size. If the subgroup samples consist of individual measurements xt, the term zt simplifies to the following computation:
is the tth subgroup average, and nt is the tth subgroup sample size. If the subgroup samples consist of individual measurements xt, the term zt simplifies to the following computation:
zt = (xt – μ0)/σ
The first equation can be rewritten as follows:
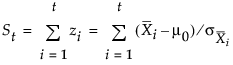
where the sequence St cumulates standardized deviations of the subgroup averages from the target mean μ0.
In many applications, the subgroup sample sizes ni are constant (ni = n), and the equation for St can be simplified, as follows:
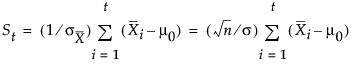
In some applications, it might be preferable to compute St as follows:
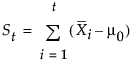
which is scaled in the same units as the data. In this case, the procedure rescales the V-mask parameters h and k to 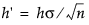 and
and 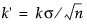 , respectively. Some authors use the symbols F for k' and H for h'.
, respectively. Some authors use the symbols F for k' and H for h'.
If the process is in control and the mean μ is at or near the target μ0, the random walk model applies. Therefore, the points might wander away from zero, but they will not exhibit a large trend since positive and negative displacements from μ0 tend to cancel each other. If μ shifts in the positive direction, the points exhibit an upward trend, and if μ shifts in the negative direction, the points exhibit a downward trend.