Canonical Details
Details for the Test Details Option
When you select the Test Details option for a given test, eigenvalues, canonical correlations, and eigenvectors are shown in the report.
The canonical correlations produced by the Test Details option are computed as follows:
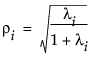
where λi is the ith eigenvalue of the E-1H matrix used in computing the multivariate test statistics
The matrix labeled Eigvec is the V matrix, which is the matrix of eigenvectors of E-1H for the given test.
Note: The E and H matrices for the given test refer to M‘EM and M‘HM in terms of the original E and H matrices. The M matrix is defined by the response design. The E and H used in this section are defined in Multivariate Tests.
Details for Centroid Plot Option
The total sample centroid and centroid values for effects are computed as follows:
Grand = 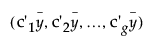
Effectj = 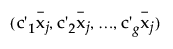
where
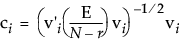
N is the number of observations
vi is the ith column of V, the eigenvector matrix of E-1H for the given test
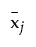 is the multivariate least squares mean for the jth effect
is the multivariate least squares mean for the jth effect
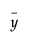 is the overall mean of the responses
is the overall mean of the responses
g is the number of eigenvalues of E-1H greater than 0
r is the rank of the X matrix
Note: The E and H matrices for the given test refer to M‘EM and M‘HM in terms of the original E and H matrices. The M matrix is defined by the response design. The E and H used in this section are defined in Multivariate Tests.
The centroid radii for effects are calculated as follows:
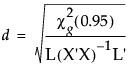
where g is the number of eigenvalues of E-1H greater than 0 and the L matrices in the denominator are from the multivariate least squares means calculations.
Details for the Save Canonical Scores Option
The canonical Y values are calculated as follows:
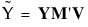
where
Y is the matrix of response variables
M’ is the transpose of the response design matrix
V is the matrix of eigenvectors of E-1H for the given test
Note: The E and H matrices for the given test refer to M‘EM and M‘HM in terms of the original E and H matrices. The M matrix is defined by the response design. The E and H used in this section are defined in Multivariate Tests.
Canonical Y values are saved for eigenvectors corresponding to eigenvalues larger than zero.