Computations for the LSN

The least significant number (LSN) solves for N in the equation:

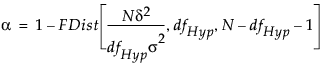
where

FDist is the cumulative distribution function of the central F distribution

dfHyp represents the degrees of freedom for the hypothesis

σ2 is the error variance

δ2 is the squared effect size

For retrospective analyses, δ2 is estimated by the sum of squares for the hypothesis divided by n, the size of the current sample. If the test is for an effect, then δ2is estimated by the sum of squares for that effect divided by the number of observations in the current study. For retrospective studies, the error variance σ2 is estimated by the mean square error. These estimates, along with an α value of 0.05, are entered into the Power Details window as default values.

When you are conducting a prospective analysis to plan a future study, consider determining the sample size that will achieve a specified power (see Computations for the Power).