Computations for the LSV
The least significant value (LSV) is computed only for a single linear contrast.
Test of a Single Linear Contrast
Consider the one-degree-freedom test Lβ = 0, where L is a row vector of constants. The test statistic for a t test for this hypothesis is:
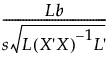
where s is the root mean square error. We reject the hypothesis at significance level α if the absolute value of the test statistic exceeds the 1 - α/2 quantile of the t distribution, t1-α/2, with degrees of freedom equal to those for error.
To find the least significant value, denoted (Lb)LSV, we solve for Lb:
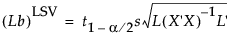
Test of a Single Parameter
In the special case where the linear contrast tests a hypothesis setting a single βi equal to 0, this reduces to the following:
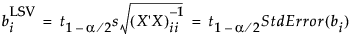
Test of a Difference in Means
In a situation where the test of interest is a comparison of two group means, the literature talks about the least significant difference (LSD). In the special case where the model contains only one nominal variable, the formula for testing a single linear contrast reduces to the formula for the LSD:
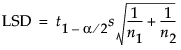
However, in JMP, the parameter associated with a level for a nominal effect measures the difference between the mean of that level and the mean for all levels. So, the LSV for such a comparison is half the LSD for the differences of the means.
Note: If you are testing a contrast across the levels of a nominal effect, keep in mind how JMP codes nominal effects. Namely, the parameter associated with a given level measures the difference to the average for all levels.