Example of a Poisson Loss Function
A Poisson distribution is often used to model count data.
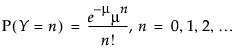
where μ can be a single parameter, or a linear model with many parameters. Many texts and papers show how the model can be transformed and fit with iteratively reweighted least squares (Nelder and Wedderburn 1972). However, in JMP it is more straightforward to fit the model directly. For example, McCullagh and Nelder (1989) show how to analyze the number of reported damage incidents caused by waves to cargo-carrying vessels.
The data are in the Ship Damage.jmp sample data table. The model formula is in the model column, and the loss function (or negative log-likelihood) is in the Poisson column. To fit the model, follow the steps below:
1. Select Help > Sample Data Library and open Ship Damage.jmp.
2. Select Analyze > Specialized Modeling > Nonlinear.
3. Assign model to the X, Predictor Formula role.
4. Assign Poisson to the Loss role.
5. Click OK.
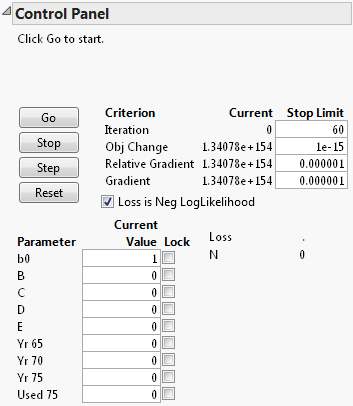
6. Set the Current Value (initial value) for b0 to 1, and the other parameters to 0.
Figure 14.15 Enter New Parameters
7. Click Go.
8. Click the Confidence Limits button.
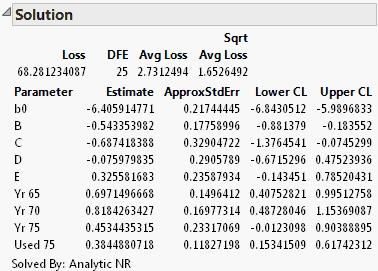
The Solution report appears. The results include the parameter estimates and confidence intervals, and other summary statistics.
Figure 14.16 Solution Table for the Poisson Loss Example