Fitting the IRT Model
The IRT model is fit using Marginal Maximum Likelihood estimation (MMLE). MMLE is an alternative method to Joint Maximum Likelihood estimation (JLE). MMLE treats the subjects as random effects. The items and abilities are related as conditional probabilities as follows:
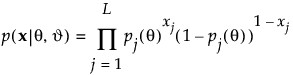
where p(x|θ, ϑ) is the probability of a response vector x given the subject ability θ and the vector of item parameters ϑ. The number of item parameters depends on the model used (1PL, 2PL, or 3PL).
MMLE integrates out the subject effects using Gaussian quadrature to obtain item parameter estimates. The probability of response vector x is as follows:
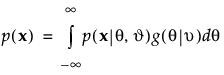
where g(θ|ν) is the distribution of the subjects and ν is a vector of the population location and scale parameters. The normal distribution with mean 0 and standard deviation 1 is used for g(θ|ν) in JMP.
Note: A missing value for a test question is treated as an incorrect response. Ability scores are not calculated for individuals with all incorrect or all correct answers. The patterns of the responses for these subjects are included in the model estimation.
The MMLE procedure for fitting the IRT model can be compared to fitting a random effects model in two stages. The ability parameters are treated as random effects with variance of 1. In the first step, these random effects are integrated out using Gaussian quadrature. The item parameters are treated as fixed effects that are estimated using ML from the marginal likelihood with the ability parameters integrated out. The ability parameters are in essence best linear unbiased predictions that are estimated using the full unintegrated (joint) likelihood, treating the item parameters as known and held fixed at the values obtained in the first stage.
There are 2L patterns of responses for L items. The ability level for each pattern can be calculated by finding the ability level with the highest probability for the response pattern by applying the following until θ converges:
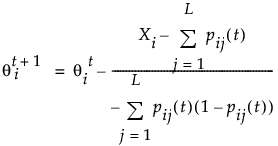
where:
θ maximizes the likelihood of obtaining the response pattern
t is the number of iterations
L is the number of items
Xi is the observed score
pij is the probability of a correct response on the jth item by the ith person based on the item parameters.