Gradients
The gradient values that you obtain when you select the Save Gradients by Subject option are the subject-aggregated Newton-Raphson steps from the optimization used to produce the estimates. At the estimates, the total gradient is zero, and Δ = H-1g = 0, where g is the total gradient of the log-likelihood evaluated at the MLE, and H-1 is the inverse Hessian function or the inverse of the negative of the second partial derivative of the log-likelihood.
But, the disaggregation of Δ results in the following:
Δ = ΣijΔij = ΣH-1gij = 0,
Here i is the subject index, j is the choice response index for each subject, Δij are the partial Newton-Raphson steps for each run, and gij is the gradient of the log-likelihood by run.
The mean gradient step for each subject is then calculated as follows:
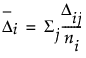 ,
,
where ni is the number of runs per subject. The Δi are related to the force that subject i is applying to the parameters. If groups of subjects have truly different preference structures, these forces are strong, and they can be used to cluster the subjects. The Δi are the gradient forces that are saved. You can then cluster these values using the Clustering platform.