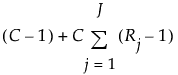Latent Class Model Fit
This section describes the latent class model that is fit in the Latent Class Analysis platform. For more information about latent class models, see Collins and Lanza (2010) and Agresti (2013).
Note: The LCA algorithm that is used in the Text Explorer platform takes advantage of the sparsity of the document term matrix. For this reason, the LCA results in the Text Explorer platform do not exactly match the results in the Latent Class Analysis platform.
Let j = 1,..., J represent the observed columns of responses. These are the Y columns in the Latent Class Analysis platform launch window. Denote the number of levels for column j by Rj.
A multidimensional contingency table of the J variables contains W = R1*...*RJ cells. Each of these cells is defined by its response pattern for the J variables. Therefore, each response pattern is a J-length vector of the form y = y1,..., yj. Define Y to be the W by J array of all the response patterns considered as row vectors. Each element, yw, in Y has a probability Pr(yw). These probabilities sum to 1:
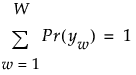
Consider the following notation:
• C is the number of clusters in the latent class model.
• γc is the probability of membership in cluster c. (The γc are the latent class prevalences.) These parameters sum to 1.
• rj,k is the kth level of the jth response.
• ρj,k|c is the probability of observing response rj,k in column j conditional on membership in class c. (The ρj,k|c are the item-response probabilities.) For a given cluster and response variable j, the sum of the ρj,k|c is 1.
• I(yj = rj,k) is an indicator function that equals 1 when the yj response is the kth level of the jth response, and 0 otherwise.
The probability of observing a specific vector of responses yw = y1,..., yj is the sum of the conditional probabilities of observing that vector of responses for each of the C latent classes:
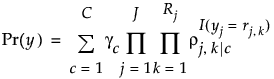
This equation is the denominator in the Prob Formula Cluster formulas that you can save to the data table by selecting the Save Mixture and Cluster Formulas option from the Latent Class Analysis red triangle menu. The formula in the Prob Formula Cluster column gives Pr(Cluster = c | yw), which equals Pr(yw, Cluster = c) / Pr(yw).
The γ and ρ parameters for latent class models are estimated using the iterative Expectation-Maximization (EM) algorithm. The number of unique parameters in a latent class model is defined as follows: