Nominal Responses
Nominal responses are analyzed with a straightforward extension of the logit model. For a binary (two-level) response, a logit response model is as follows:
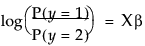
The above can also be written as follows:
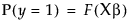
where F(x) is the cumulative distribution function of the standard logistic distribution:
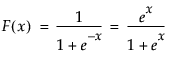
For r response levels, JMP fits the probabilities that the response is one of r different response levels given by the data values. The probability estimates must all be positive. For a given configuration of Xs, the probability estimates must sum to 1 over the response levels. The function that JMP uses to predict probabilities is a composition of a linear model and a multi-response logistic function. This is sometimes called a log-linear model because the logs of ratios of probabilities are linear models. JMP relates each response probability to the rth probability and fit a separate set of design parameters to these r - 1 models.
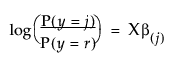 for
for 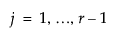
Fitting Principle for Nominal Response
The fitting principle is called maximum likelihood. It estimates the parameters such that the joint probability for all the responses given by the data is the greatest obtainable by the model. Rather than reporting the joint probability (likelihood) directly, it is more manageable to report the total of the negative logs of the likelihood.
The uncertainty (negative log-likelihood) is the sum of the negative logs of the probabilities attributed by the model to the responses that actually occurred in the sample data. For a sample of size n, it is often denoted as H and written
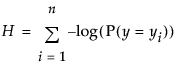
If you attribute a probability of 1 to each event that did occur, then the sum of the negative logs is zero for a perfect fit.
The nominal model can take a lot of time and memory to fit, especially if there are many response levels. JMP tracks the progress of its calculations with an iteration history, which shows the negative log-likelihood values becoming smaller as they converge to the estimates.
Base Model for Nominal Responses
The simplest model for a nominal response is a set of constant response probabilities fitted as the occurrence rates for each response level across the whole data table. In other words, the probability that y is response level j is estimated by dividing the total sample count n into the total of each response level nj. This probability is written as follows:
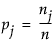
All other models are compared to this base model. The base model serves the same role for a nominal response as the sample mean does for continuous models.
The R2 statistic measures the portion of the uncertainty accounted for by the model, which is
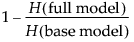
However, it is rare in practice to get an R2 near 1 for categorical models.