Overview of the Factor Analysis Platform
Factor analysis models a set of observable variables in terms of a smaller number of unobservable factors. The factors are constructed to account for the correlation or covariance between the observed variables. Factor rotation is used to change the reference axes of the factors to increase their interpretability.
Consider a situation where you have ten observed variables, X1, X2, …, X10. Suppose you want to model these ten variables in terms of two latent factors, F1 and F2. For convenience, it is assumed that the factors are uncorrelated and that each has mean zero and variance one. The model that you want to derive is of the form:
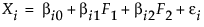
It follows that Var(Xi) = βi12 + βi22 + Var(εi). The portion of the variance of Xi that is attributable to the factors, the common variance or communality, is βi12 + βi22. The remaining variance, Var(εi), is the unique variance, and is considered to be a combination of specific and error variances that are unique to Xi.
The platform provides a scree plot for the eigenvalues of the correlation or covariance matrix. You can use this as a guide in determining the number of factors to extract. The platform's default number of factors is the number of eigenvalues that exceed one.
The platform provides two factoring methods for estimating the parameters of this model: Principal Axis and Maximum Likelihood. There are two Prior Communality options for estimating the proportion of variance contributed by common factors for each variable. These options impose assumptions on the diagonal of the correlation (or covariance) matrix. The Principal Components option treats the correlation matrix, which has ones on its diagonal (or the covariance matrix with variances on its diagonal), as the structure to be analyzed. The Common Factor Analysis option sets the diagonal entries to square multiple correlations. These are values that reflect the proportion of the variation shared with other variables.
Factor rotation is used to support interpretability of the extracted factors. The Factor Analysis platform provides a variety of rotation methods that encompass both orthogonal and oblique rotations.
In contrast to factor analysis, which looks at common variance, principal component analysis accounts for the total variance of the observed variables. See Principal Components.
For more information about factor analysis, see Jöreskog (1977) or Cudeck and MacCallum (2007).