Statistical Details for ARIMA Models
ARIMA Model
For a response series {yi}, the general form for the ARIMA model is as follows:
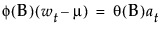
where
t is the time index
B is the backshift operator defined as Byt = yt - 1
wt = (1 - B)d yt is the response series after differencing
μ is the intercept or mean term
φ(B) and θ(B) are the autoregressive operator and the moving average operator, respectively, and are written as follows:
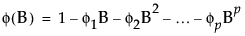
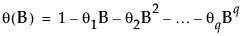
where
at are the sequence of random shocks
The at are assumed to be independent and normally distributed with mean zero and constant variance.
The model can be rewritten as follows:
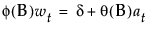
The constant estimate δ is given by the relation:
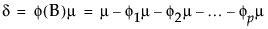
Seasonal ARIMA Model
In the case of Seasonal ARIMA modeling, the differencing, autoregressive, and moving average operators are the product of seasonal and nonseasonal polynomials:
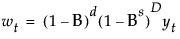
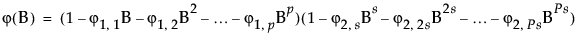
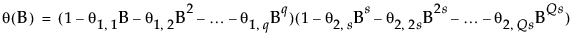
where s is the number of observations per period. The first index on the coefficients is the factor number (1 indicates nonseasonal, 2 indicates seasonal) and the second is the lag of the term.