Statistical Details for Balanced Incomplete Block Designs
The total number of observations in a BIBD is determined by the following equation:
N = ar = bk
where
a is the number of treatments
r is the number of times each treatment occurs in the design
b is the number of blocks
k is the number of treatments in each block
The number of blocks in which each pair of treatments occurs is given by the following:
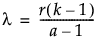
where λ must be an integer.
These conditions are necessary for a BIBD to exist, but not sufficient. The BIBD platform presents values for which it can generate a BIBD.
When the Include Block Multiples is selected, the original BIBD is copied the number of times specified. The additional (multiple) blocks are cyclic permutations of the original design. The positions of treatments in the copies differs from the original.
For more information about BIBDs, see SAS Institute Inc. (2013).