Statistical Details for Continuous Fit Distributions (Legacy)
This section contains statistical details for the options in the Continuous Fit menu.
Note: Some features of distribution fitting have been updated in JMP 15. This section contains details of the older features from previous JMP releases that have been retained for compatibility purposes. These features are available by selecting Continuous Fit > Enable Legacy Fitters in the red triangle menu for a variable.
Normal
For more information about the normal distribution fit, see Fit Normal.
LogNormal
For more information about the lognormal distribution fit, see Fit Lognormal.
Weibull, Weibull with Threshold, and Extreme Value
The Weibull distribution has different shapes depending on the values of α (scale) and β (shape). It often provides a good model for estimating the length of life, especially for mechanical devices and in biology.
The pdf for the Weibull and Weibull with Threshold distributions is as follows:
pdf: 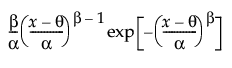 for α,β > 0; θ < x
for α,β > 0; θ < x
E(x) = 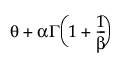
Var(x) = 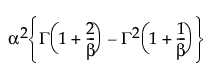
where Γ(·) is the Gamma function.
The Weibull option sets the threshold parameter (θ) to zero. The Weibull with Threshold option, estimates the threshold parameter (θ) using the value of the minimum observation and estimates α and β using the rest of the observations. If you know what the threshold should be, set it by using the Fix Parameters option. See Fit Distribution Options.
Note: The Distribution platform uses a different estimation technique for the threshold parameter in the Weibull with Threshold distribution than does the Life Distribution platform. The Life Distribution estimation method is recommended for fitting this distribution. See Statistical Details for the Life Distribution Platform in Reliability and Survival Methods.
The Extreme Value distribution is equivalent to a two-parameter Weibull (α, β) distribution re-parameterized as δ = 1 / β and λ = ln(α).
Exponential
For more information about the exponential distribution fit, see Fit Exponential.
Gamma
The Gamma fitting option estimates the gamma distribution parameters, α > 0 and σ > 0. The parameter α, called alpha in the fitted gamma report, describes shape or curvature. The parameter σ, called sigma, is the scale parameter of the distribution. A third parameter, θ, called the Threshold, is the lower endpoint parameter. It is set to zero by default, unless there are negative values. You can also set its value by using the Fix Parameters option. See Fit Distribution Options.
pdf: 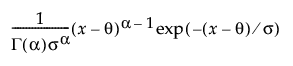 for 0 ≤ x; 0 < α,σ
for 0 ≤ x; 0 < α,σ
E(x) = ασ + θ
Var(x) = ασ2
• The standard gamma distribution has σ = 1. Sigma is called the scale parameter because values other than 1 stretch or compress the distribution along the horizontal axis.
• The Chi-square 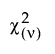 distribution occurs when σ = 2, α = ν/2, and θ = 0.
distribution occurs when σ = 2, α = ν/2, and θ = 0.
• The exponential distribution is the family of gamma curves that occur when α = 1 and θ = 0.
The standard gamma density function is strictly decreasing when α ≤ 1. When α > 1, the density function begins at zero, increases to a maximum, and then decreases.
Beta
The standard beta distribution is useful for modeling the behavior of random variables that are constrained to fall in the interval 0,1. For example, proportions always fall between 0 and 1. The Beta fitting option estimates two shape parameters, α > 0 and β > 0, and two threshold parameters, θ and σ. The lower threshold is represented as θ, and the upper threshold is represented as θ + σ. The beta distribution has values only in the interval θ ≤ x ≤ (θ + σ). The θ is estimated by the minimum value, and σ is estimated by the range. The standard beta distribution occurs when θ = 0 and σ = 1.
Set parameters to fixed values by using the Fix Parameters option. The upper threshold must be greater than or equal to the maximum data value, and the lower threshold must be less than or equal to the minimum data value. For more information about the Fix Parameters option, see Fit Distribution Options.
pdf: 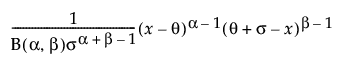 for θ ≤ x ≤ θ + σ; 0 < σ,α,β
for θ ≤ x ≤ θ + σ; 0 < σ,α,β
E(x) = 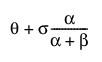
Var(x) = 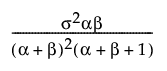
where B(·) is the Beta function.
Normal Mixtures
For more information about the normal mixtures distribution fits, see Fit Normal 2 Mixture and Fit Normal 3 Mixture.
Smooth Curve
The Smooth Curve option fits a smooth curve using nonparametric density estimation (kernel density estimation). The smooth curve is overlaid on the histogram and a slider appears beneath the plot. Control the amount of smoothing by changing the kernel standard deviation with the slider. The initial Kernel Std estimate is calculated from the standard deviation of the data.
SHASH
For more information about the SHASH distribution fit, see Fit SHASH.
Johnson Su, Johnson Sb, Johnson Sl
The Johnson system of distributions contains three distributions that are all based on a transformed normal distribution. These three distributions are the following:
• Johnson Su, which is unbounded.
• Johnson Sb, which has bounds on both tails. The bounds are defined by parameters that can be estimated.
• Johnson Sl, which is bounded in one tail. The bound is defined by a parameter that can be estimated. The Johnson Sl family contains the family of lognormal distributions.
The S refers to system, the subscript of the range. Although we implement a different method, information about selection criteria for a particular Johnson system can be found in Slifker and Shapiro (1980).
Johnson distributions are popular because of their flexibility. In particular, the Johnson distribution system is noted for its data-fitting capabilities because it supports every possible combination of skewness and kurtosis.
If Z is a standard normal variate, then the system is defined as follows:
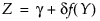
where, for the Johnson Su:
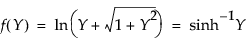
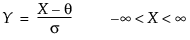
where, for the Johnson Sb:
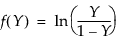
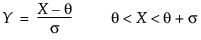
and for the Johnson Sl, where σ = ±1.
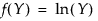
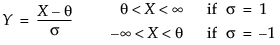
Johnson Su
pdf: 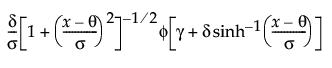 for -∞ < x, θ, γ < ∞; 0 < θ,δ
for -∞ < x, θ, γ < ∞; 0 < θ,δ
Johnson Sb
pdf: 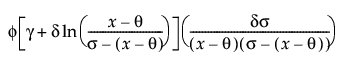 for θ < x < θ+σ; 0 < σ
for θ < x < θ+σ; 0 < σ
Johnson Sl
pdf: 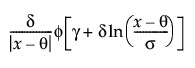 for θ < x if σ = 1; θ > x if σ = -1
for θ < x if σ = 1; θ > x if σ = -1
where φ(·)is the standard normal pdf.
Note the following:
• Parameter estimates might be different between machines due to the order of operations and machine precision.
• The parameter confidence intervals are hidden in the default report. Parameter confidence intervals are not very meaningful for Johnson distributions, because they are transformations to normality. To show parameter confidence intervals, right-click in the report and select Columns > Lower 95% and Upper 95%.
Generalized Log (Glog)
This distribution is useful for fitting data that are rarely normally distributed and often have non-constant variance, like biological assay data. The Glog distribution is described with the parameters μ (location), σ (scale), and λ (shape).
pdf: 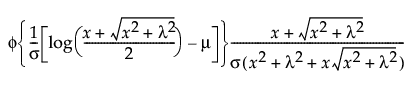
for 0 ≤ λ; 0 < σ; -∞ < μ < ∞
The Glog distribution is a transformation to normality, and comes from the following relationship:
If z = 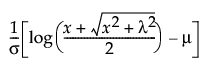 ~ N(0,1), then x ~ Glog(μ,σ,λ).
~ N(0,1), then x ~ Glog(μ,σ,λ).
When λ = 0, the Glog reduces to the LogNormal (μ,σ).
Note: The parameter confidence intervals are hidden in the default report. Parameter confidence intervals are not very meaningful for the GLog distribution, because it is a transformation to normality. To show parameter confidence intervals, right-click in the report and select Columns > Lower 95% and Upper 95%.
All
In the Compare Distributions report, the Distribution list is sorted by AICc in ascending order.
The formula for AICc is as follows:
AICc = 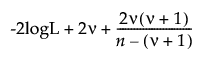
where:
– logL is the log-likelihood.
– n is the sample size.
– ν is the number of parameters.
If the column contains negative values, the Distribution list does not include those distributions that require data with positive values. Only continuous distributions are listed. Distributions with threshold parameters, such as Beta and Johnson Sb, are not included in the list of possible distributions.