Statistical Details for the Counts per Unit Calculator
Calculations for the counts per unit calculator are based on applying a normal approximation to the Poisson distribution. The test uses the following hypothesis:
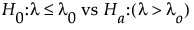
The above hypothesis uses the following test statistic:
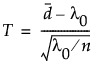
where n is the sample size and 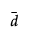 is the mean number of defects per unit in the sample. We assume T to be approximately normally distributed. The power calculation is based on the distribution of T under the null and alternative hypotheses.
is the mean number of defects per unit in the sample. We assume T to be approximately normally distributed. The power calculation is based on the distribution of T under the null and alternative hypotheses.
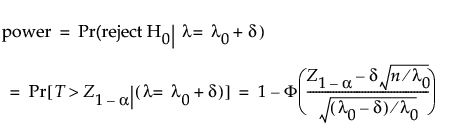
where Φ() is the standard normal cumulative distribution function and Z1-p is the (1 - p)th quantile of the standard normal distribution.
Using 1 - β to denote the desired power to reject the null hypothesis, the sample size is calculated as follows:
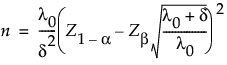
Because an analytical solution for δ does not exist, numerical methods are used to solve for δ given power and n.
For more information about calculations in JMP, see Barker (2011, Section 2.5).