Uncertainty, a Unifying Concept
When you do accounting, you total money amounts to get summaries. When you look at scientific observations in the presence of uncertainty or noise, you need some statistical measurement to summarize the data. Just as money is additive, uncertainty is additive if you choose the right measure for it.
The best measure is not the direct probability because to get a joint probability, you have to assume that the observations are independent and then multiply probabilities rather than add them. It is easier to take the log of each probability because then you can sum them and the total is the log of the joint probability.
However, the log of a probability is negative because it is the log of a number between 0 and 1. In order to keep the numbers positive, JMP uses the negative log of the probability. As the probability becomes smaller, its negative log becomes larger. This measure is called uncertainty, and it is measured in reverse fashion from probability.
In business, you want to maximize revenues and minimize costs. In science, you want to minimize uncertainty. Uncertainty in science plays the same role as cost plays in business. All statistical methods fit models such that uncertainty is minimized.
It is not difficult to visualize uncertainty. Just think of flipping a series of coins where each toss is independent. The probability of tossing a head is 0.5, and -log(0.5) is 1 for base 2 logarithms. The probability of tossing h heads in a row is as follows:
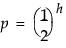
Solving for h produces the following:
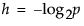
You can think of the uncertainty of some event as the number of consecutive “head” tosses you have to flip to get an equally rare event.
Almost everything we do statistically has uncertainty, -logp, at the core. Statistical literature refers to uncertainty as negative log-likelihood.