Convergence Score Test
The convergence failure warning shows the score test for the following hypothesis: that the unknown maximum likelihood estimate (MLE) is consistent with the parameter given in the final iteration of the model-fitting algorithm. This hypothesis test is possible because the relative gradient criterion is algebraically equivalent to the score test statistic. Remarkably, the score test does not require knowledge of the true MLE.
Score Test
Consider first the case of a single parameter, θ. Let l be the log-likelihood function for θ and let x be the data. The score is the derivative of the log-likelihood function with respect to θ:
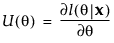
The observed information is:
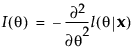
The statistic for the score test of H0: θ = θ0 is:
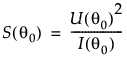
This statistic has an asymptotic Chi-square distribution with 1 degree of freedom under the null hypothesis.
The score test can be generalized to multiple parameters. Consider the vector of parameters θ. Then the test statistic for the score test of H0: θ = θ0 is:
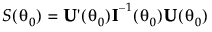
where
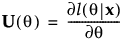
and
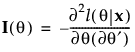
and U′ denotes the transpose of the matrix U.
The test statistic is asymptotically Chi-square distribution with k degrees of freedom. Here k is the number of unbounded parameters.
Relative Gradient
The convergence criterion for the Mixed Model fitting procedure is based on the relative gradient g′H−1g. Here, g(θ) = U(θ) is the gradient of the log-likelihood function and H(θ) = −I(θ) is its Hessian.
Let θ0 be the value of θ where the algorithm terminates. Note that the relative gradient evaluated at θ0 is the score test statistic. A p-value is calculated using a Chi-square distribution with k degrees of freedom. This p-value gives an indication of whether the value of the unknown MLE is consistent with θ0. The number of unbounded parameters listed in the Random Effects Covariance Parameter Estimates report equals k.