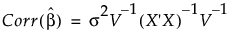Correlation of Estimates
Consider a data set with n observations and p - 1 predictors. Define the matrix X to be the design matrix. That is, X is the n by p matrix whose first column consists of 1s and whose remaining p - 1 columns consist of the p - 1 predictor values. (Nominal columns are coded in terms of indicator predictors. Each of these is a column in the matrix X.)
The estimate of the vector of regression coefficients is
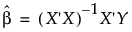
where Y represents the vector of response values.
Under the usual regression assumptions, the covariance matrix of 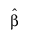 is
is
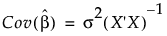
where σ2 represents the variance of the response.
The correlation matrix for the estimates is obtained by dividing each entry in the covariance matrix by the product of the square roots of the diagonal entries. Define V to be the diagonal matrix whose entries are the square roots of the diagonal entries of the covariance matrix:
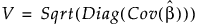
Then the correlation matrix for the parameter estimates is given by the following: