Example of Balanced Incomplete Block Designs
In this example, you want to test three new product formulations in your plant, and you want to block by day. There is a limit of two formulations that can be run per day. In addition, you need to finish your experiment in one work week. You need a design with at most five blocks.
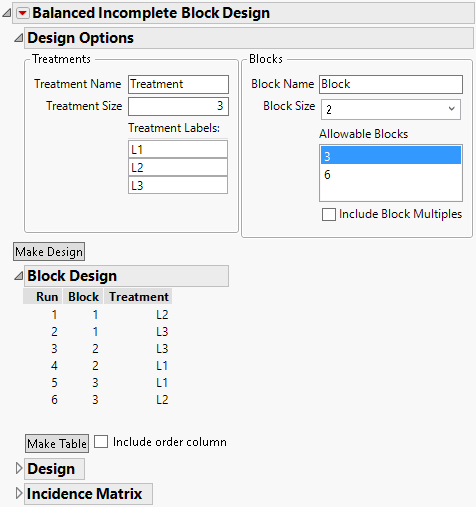
1. Select DOE > Special Purpose > Balanced Incomplete Block Design.
2. Set the Treatment Size to 3.
Tip: Treatment size can refer to the number of levels of a single factor or combinations of levels of two or more factors.
3. Select 2 for the Block Size.
4. Select 3 for Allowable Blocks.
You can select 3 or 6 blocks. In this example, each block is a day and you can have no more than 5 days or 5 blocks. The number of runs is 6 because you have 3 blocks of size 2.
Note: You can enter a Treatment Name, Block Name, and Treatment Labels to customize your design table.
5. Click Make Design.
Figure 24.2 BIBD for 3 Treatments in 3 Blocks of Size 2
The design has six runs in three blocks with two treatments in each block as seen in the Block Design outline. For additional design details open the Design and Incidence Matrix outlines. See Verify Design and Make Table.
Initially, you had to select a design with 3 or 6 blocks. You selected 3 blocks because of time constraints in your plant. However, suppose you were allowed to run your experiment for 6 days. You could then update the design to use 6 blocks.
6. Select 6 in the Allowable Blocks menu.
7. Click Make Design to update the design.
8. Open the Incidence Matrix outline.
Figure 24.3 BIBD Design Details for 3 Treatments in 6 Blocks of Size 2
Now the design has 6 blocks. The incidence matrix shows the treatments that are in each block. The Pairwise Treatment Frequencies shows that each treatment appears four times (diagonal entries) and that each treatment pair occurs twice in the design (off diagonal entries). The blocks each have two positions. The Positional Frequencies show that treatment L1 always occurs in position 1, L2 is split between the two positions, and L3 occurs in position 2.